TiZrTaMoNb高熵合金动态特性与应用研究

发布时间:

2025-07-16

0 引言
自1888年由Munroe［1］发现聚能效应后，聚能装药就被广泛应用于弹药战斗部和工程领域。经过几个世纪的发展，聚能装药在战斗部中的应用现主要分为聚能射流(JET)、聚能杆式弹丸(JPC)、爆炸成型弹丸(EFP)三种类型。
聚能装药的成型和毁伤效果受药型罩材料、装药结构和药型罩形状等多个因素共同影响。目前对药型罩材料的研究主要集中在以下两个方面:一是对新材料应用于药型罩的可行性进行探索;二是对常用药型罩材料的制作工艺进行优化，以提升聚能装药性能。在研究新材料应用于药型罩的可行性时，主要考虑密度、声速、物理对称性和几何对称性这4个基本要素［2］。相较于JET和JPC，EFP战斗部在成型过程中的变形往往相对较小，较少发生类似流体一般的极端大变形，所以EFP战斗部对于药型罩材料延展性的要求也相应稍低。在EFP战斗部侵彻过程中，往往将其近似为动能弹进行处理，对材料的密度和强度有较高要求。因此，在对药型罩选材的具体要求上，EFP战斗部与JET和JPC存在一定区别。
高熵合金(High-entropyalloys)又被称为多主元合金，可以通过对不同组分进行原子级别配比，达到对密度、延展性、强度、含能量等重要参数的调控能力。鉴于高熵合金优异的性能，已有部分学者对高熵合金在战斗部上的应用进行了研究，其中部分将其作为战斗部壳体材料［4］或动能弹体材料［5－6］，还有部分学者将轻质高熵合金用作聚能射流药型罩材料［7］，均达到了较好的效果。本文中所研究的TiZrTa-MoNb高熵合金为等原子比制作的Ti-Zr系难溶高熵合金，密度为9．118g/cm3，与目前常用的药型罩材料—紫铜(8．9g/cm3)相当。Ti-Zr系难溶高熵合金的屈服强度约在1000～2000MPa［3］，但由于加入了Mo和Nb，其强度应有所降低，根据准静态压缩试验结果，TiZrTaMoNb高熵合金在静态压缩时，屈服强度约为859MPa。由以上数据来看，其强度和密度满足作为EFP药型罩材料的基本要求，由于缺少拉伸实验，无法对TiZrTaMoNb高熵合金的延展性进行较为直观的评价。因此结合几种同类型高熵合金的断裂延伸率和压缩实验中的失效应变参数，对TiZrTaMoNb高熵合金的延展性作粗略估计。
根据现有报道，TaNbTiZr难熔高熵合金［8］断裂伸长率约为3．99%;等原子比的TiZrNbHfTa高熵合金［9］屈服强度、极限断裂强度分别达到1170、1260MPa，断裂延伸率8%，表现出优异的强度-塑性协同效应;由Juan等［10］制备HfMoN-bTaTiZr难熔高熵合金在室温下仍能保持12%的断裂延伸率，并且随着温度升高而提高，在1200℃下达到30%，表现出较明显的温度软化现象。根据静、动态压缩实验结果，TiZrTaMoNb高熵合金在准静态压缩时，失效应变约为29.4%;在进行动态压缩实验时，当应变率从851s－1上升到2403s－1，最大应变从12．6%上升到33．8%，在此过程中试件均未产生裂纹，表现出较好的延展性。
综合静、动态压缩试验结果和以上学者研究内容，TiZr-TaMoNb高熵合金存在作为药型罩材料的可能性，因此对TiZrTaMoNb高熵合金应用于EFP药型罩材料的可行性进行了研究。
1 试验研究
1．1 试验设置
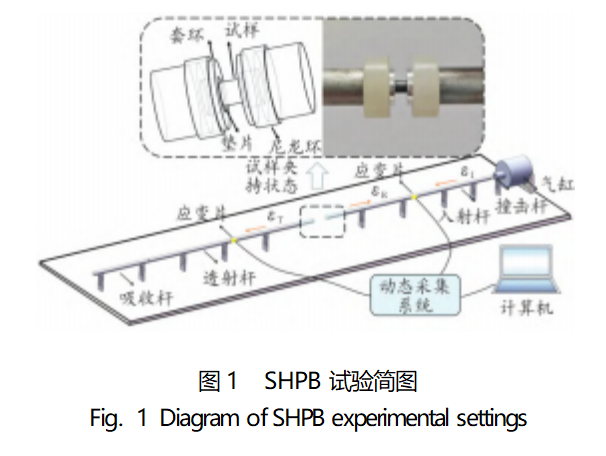
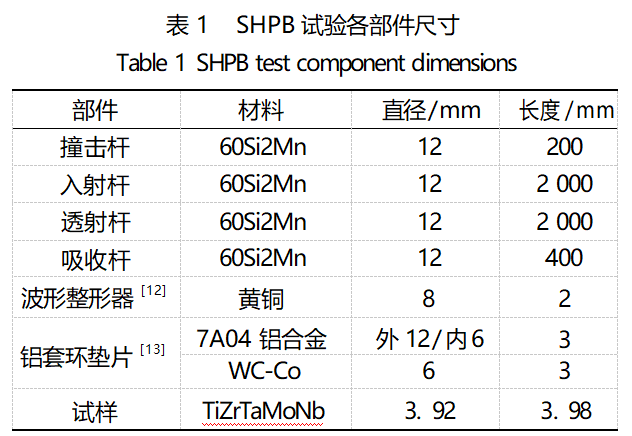
准静态压缩试验采用万能试验机，应变率为0．001s－1，采样频率为1MHz。动态压缩试验使用SHPB进行，参考文献［11］进行设置;共进行4组动态压缩试验，SHPB试验简图如图1所示，试验各部分尺寸和材料如表1所示。

1．2 试验结果及数据处理
SHPB试验测试原理如图2所示，当试件处于应力平衡状态时，平均工程应变率和应变由式(1)和式(2)进行计算:

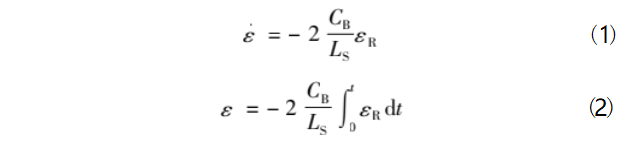
其中:LS为试件的初始长度;v1、v2分别为入射杆、透射杆质点运动速度;εI、εR、εT分别为入射波、反射波和透射波;CB为杆材料的波速。

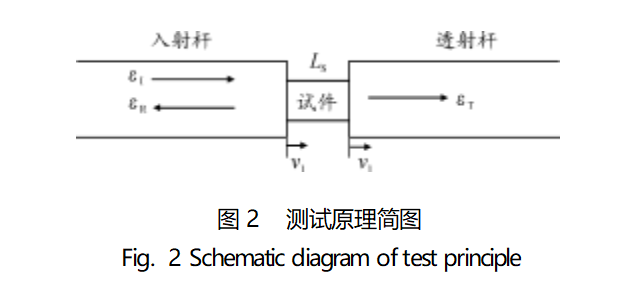
试件两端应力由下列弹性关系计算获得［14］:

式中:AB、AS分别为杆与试件的横截面积;EB为杆材料的弹性模量。
通过上述公式对试验结果进行处理，将各应变率下应力－应变曲线绘制如图3所示，屈服强度、最大应力及最大应变列在表2。

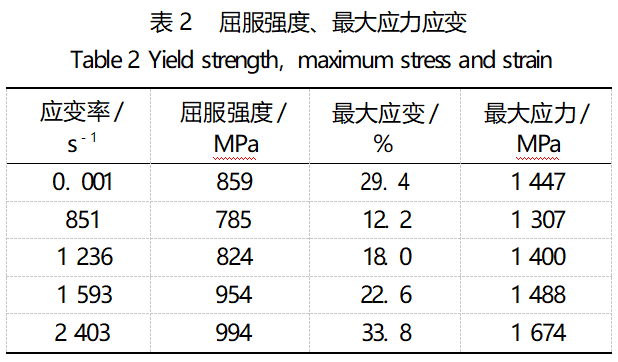
由图3可以看出，当应变率从851s－1增加到2403s－1时，屈服强度从785MPa升高到994MPa，最大应变由12.2%升高到33．8%，体现出较明显的应变率效应。
2 本构模型参数拟合
2．1 本构模型的选取
EFP成型是一个高应变率的过程，需要选取一个合适的材料模型来描述材料在高应变率条件下的应力－应变关系和应变率效应。Johnson-Cook模型［15］囊括了应变、应变速率和温度因素对大多数金属材料的影响，因其形式简单、物理意义明确、参数易于测试和校准的特点，被广泛应用于爆炸与冲击领域。因此，选择Johnson-Cook模型描述TiZrTaMoNb高熵合金在冲击响应情况下的应力－应变关系，本构模型由应变硬化、应变速率敏感性和温度3个乘法项定义，其定义如下:

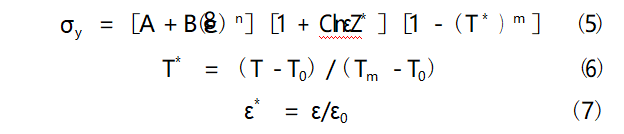
其中:为等效塑性应变，ε*为无量纲塑性应变率，ε0为参考
应变率(参考应变率取准静态加载时应变率);T*为相对温度，T0为参考温度(一般为室温)，Tm为融化温度，T为瞬时温度。A、B、n、C、m为待拟合的参数。
2．2本构模型参数拟合
2．2．1参数拟合方法
A、B、n三个参数描述的是材料在某一固定应变率下，屈服点处和塑性变形阶段的应力－应变关系。一般根据准静态、室温加载条件下的应力－应变曲线对A、B、n进行拟合。准静态加载状态下，应变率为0．001s－1，取室温，因此，式(5)可以简化为

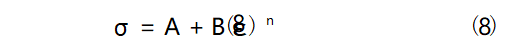
在初始屈服点，此时可看作还未发生塑性应变，ε=0。此时，A即为屈服强度，对塑性阶段应力－应变曲线拟合即可确定B、n的值。
C可由室温时不同应变率对应的屈服强度值拟合确定，此时方程变为

2．2．2参数拟合结果
以室温准静态加载条件下的应变率为参考应变率(0．001s－1)，由参考应变率下的应力－应变塑性段曲线对参数
A、B、n进行拟合，拟合结果如图4所示。
由图4可以看出，TiZrTaMoNb高熵合金在室温准静态加载下(应变率0．001s－1)屈服强度为859MPa，即A值为859MPa。固定A值，对应力－应变曲线塑性阶段拟合可得参数B为2051MPa，n值为0．88093。
根据式(9)，采用单线程确定动态压缩试验屈服强度的方法，对参数C进行拟合，拟合结果如图5所示。

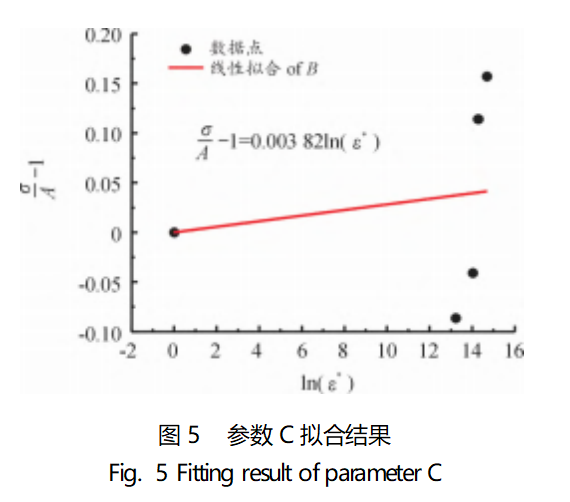
由图5可以看出，拟合曲线斜率为0．00382，即参数C为0．00382。由于拟合过程忽略温度变化对材料应变效应造成的影响，因此，其本构模型方程(忽略温度项)如下所示:
σy=(859+2051ε0．88093)(1+0．0382lnε*)(10)
由图5可以看出，参数C的拟合结果线性度较差，为了对参数C的有效性进行粗略估计，选取数个应变数据点，将其代入式(10)中进行计算，将计算结果和实验曲线进行比较并绘制如图6所示。

由图6可以看出，使用拟合参数取点计算的结果和试验所得曲线存在较大差距，无法体现出材料的应变率效应。由图5也可以看出，参数C的线性拟合曲线和各数据点之间关系度较差，线性拟合曲线无法代表每个应变率的应力－应变情况。主要表现在各应变率的近似计算结果差距不大，看起来像是“挤”在一起。出现这种情况的主要原因是控制应变率效应的参数C不够准确，不能真实反映材料的应变率效应。
根据式(9)，参数C体现的是各应变率和参考应变率下屈服强度的比值与各应变率和参考应变率之间比值的线性关系。参数C受到参考应变率、各动态压缩试验应变率、参考应变率下屈服强度A和各动态应变率下屈服强度σ的共同影响。由图3、图4可以看出，不论是动态压缩还是静态压缩，其应力应变曲线都存在2个折点;并且较明显的是，动态压缩在弹性段后还有一段强化阶段，并不是直接进入塑性变形阶段，在这一阶段内，应力和应变都还有较明显的变化，如果使用单线程的方法来确定屈服强度，就会导致在屈服点后就直接进入塑性变形阶段，缺少了强化阶段的应力变化，导致应力偏小，如图6所示。
为了解决这一问题，使用双线程确定屈服强度的方法对参数C进行重新拟合，双线程方法确定屈服强度结果如表3所示。

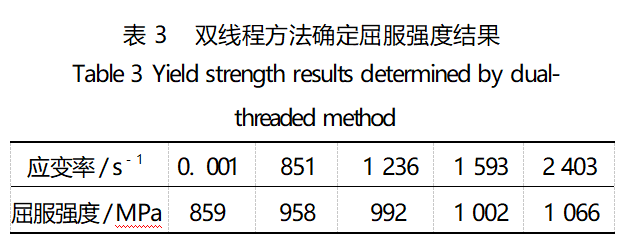
参数C重新拟合结果如图7所示，对参数C重新拟合后取点计算结果如图8所示。

比较图7、图8和图5、图6可以看出，重新拟合后参数C的线性度以及近似计算的结果均要优于原来，更接近试验效果，能够反映材料的应变率效应。重新拟合后的本构模型方程如式(11)所示。

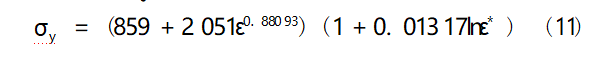
2．3 状态方程参数拟合
Grunisen状态方程用于描述材料受到冲击波作用时的状态变化。该状态方程考虑了材料在冲击波加载下表现出的非线性、非平衡特性，以及高温高压的影响，能够有效地表征材料的状态变化。在冲击加载下，材料中冲击波波前的传播速度与后方粒子运动速度之间的关系可以用式(12)、式(13)表示。

式中:U为冲击波前沿的传播速度，C0为材料在室温下的体声速，S为线性雨贡尼奥梯度，up为波后粒子运动的速度。

式中:γ=B0/(1+μ)，μ为材料泊松比，B0为常数;pH为雨贡尼奥压力;eH为雨贡尼奥能。
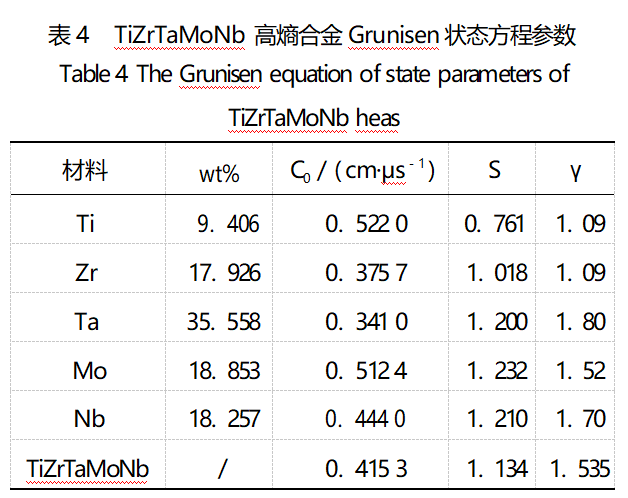
由于缺少TiZrTaMoNb高熵合金相关的平板撞击试验，因此采用Voigt-Reuss-Hill［16－17］混合规则对TiZrTaMoNb高熵合金的Grunisen状态方程参数进行近似计算，计算方法如式(14)所示。各金属单质和近似计算的TiZrTaMoNb高熵合金的Grunisen状态方程参数如下表4所示。

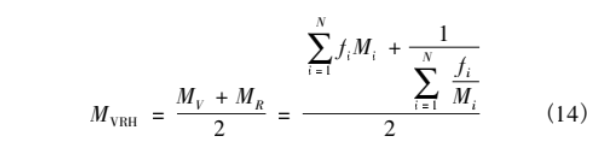
式中:fi为组分的质量分数;Mi为各组分的参数。

3 模型验证
3．1 数值模型
为了验证拟合参数的准确性，使用LS-DYNA有限元仿真软件进行数值模拟。根据SHPB试验等比例建立1/4三维有限元模型，各端面间采用(SURFACE-To-SURFACE)面-面接触，使用3DSolid164六面体单元对模型进行网格划分，网格划分情况如图9所示。

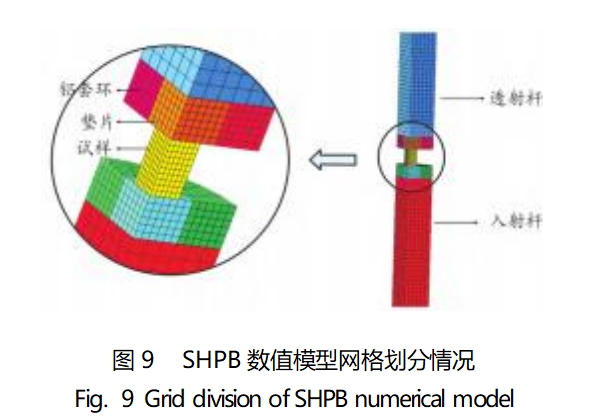
由SHPB试验理论可知，入射波在杆件中以弹性波传播［14］，因此选用式(15)将应变片所测得电压信号转化为应力－时间变化曲线加载到模型上。

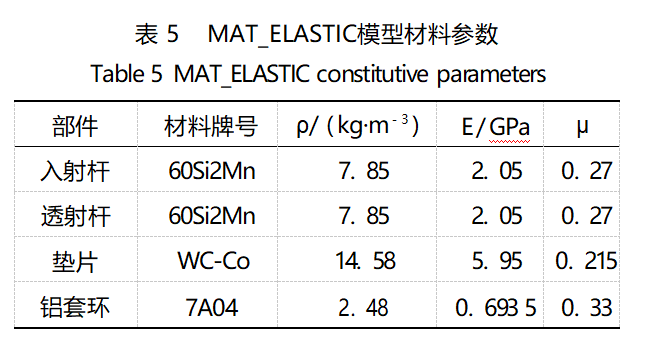
其中，钢杆、垫片及铝套环均选用MAT_ELASTIC材料模型，主要材料参数如表5所示。TiZrTaMoNb高熵合金试样选用Johnson-Cook本构模型，配合Gruneisen状态方程，主要材料参数如表6所示。

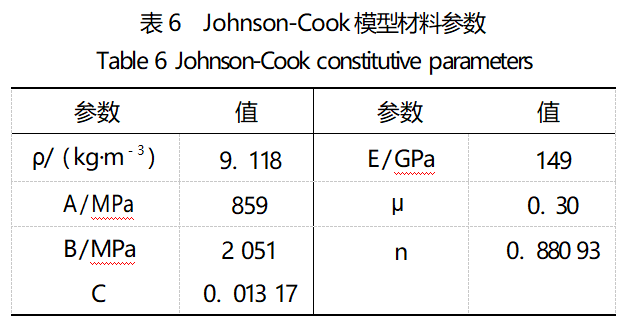
注:ρ为密度;E为弹性模量;μ为泊松比;A、B、n、C为拟合参数;εZ0为参考应变率。
3．2 数值模拟结果
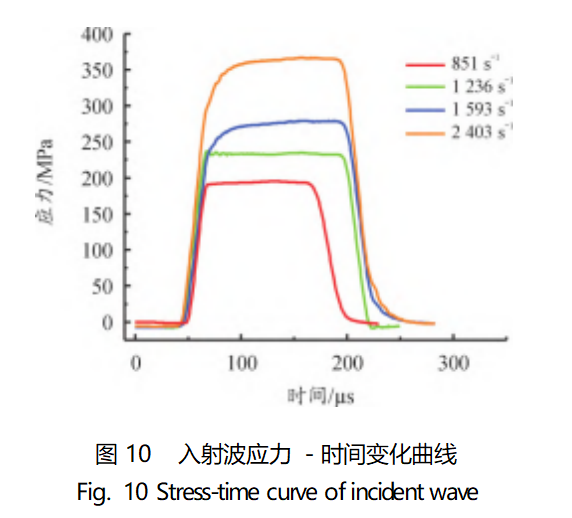
根据式(14)计算得到的入射波应力－时间变化曲线如图10所示。将入射波加载到入射杆端面，对4次动态压缩试验(应变率851、1236、1593、2403s－1)进行数值模拟验证，数值模拟所得应力－应变曲线如图11所示。

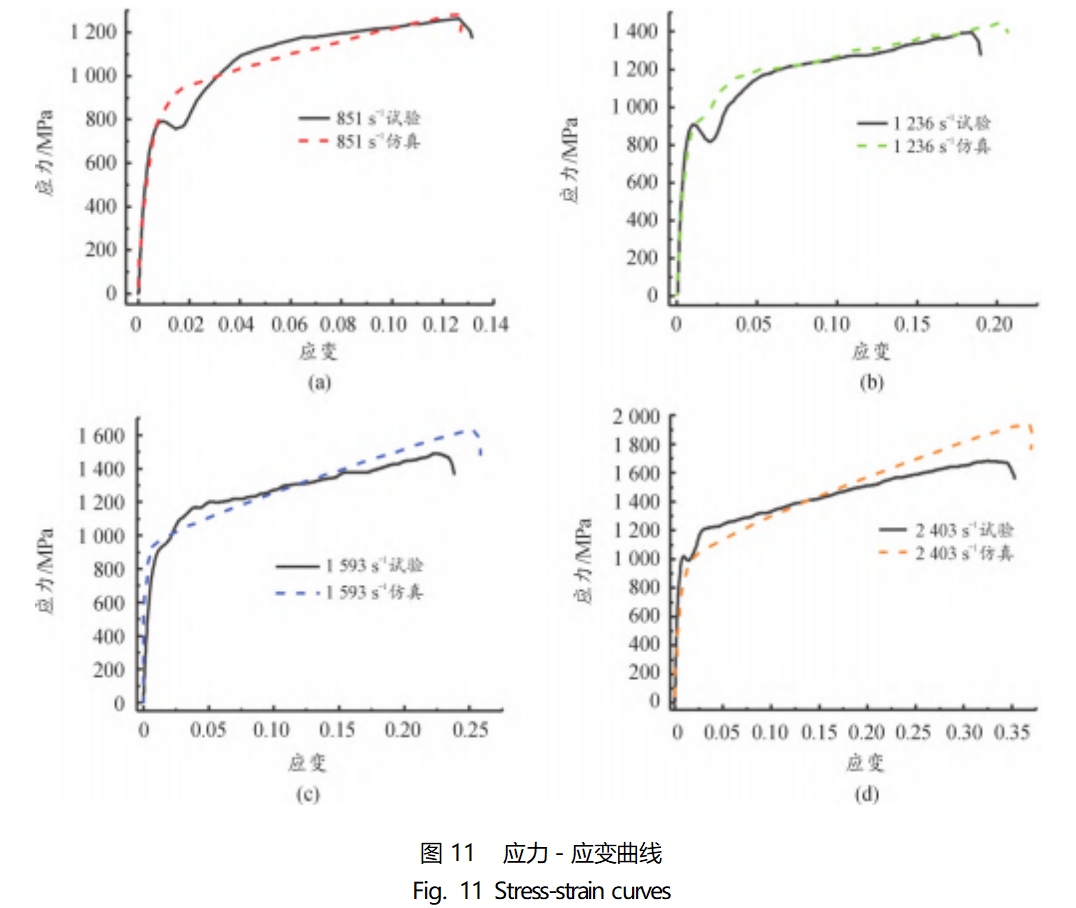
由图11可以看出，通过仿真模型计算出来的应力－应变曲线和试验之间总是存在一定的误差，误差主要来自于以下3个方面:一是在试验数据得到的曲线中，在屈服点后有较明显的强化阶段，使用Johnson-Cook材料模型无法体现出这一变化;二是静态压缩(0．001s－1)和动态压缩在塑性变形阶段的曲线斜率本就存在一定差异，这个差异直接导致由参考应变率拟合得到的A、B、n参数在用于高应变率的仿真时会出现一定的误差;三是应变率强化效应在影响应力变化时不明显，这是由于参数C在拟合过程中也存在一定误差。
选取屈服强度、最大应力、最大应变3个参数作为计算误差的指标，计算各应变率下仿真与试验之间的误差并列在表7。

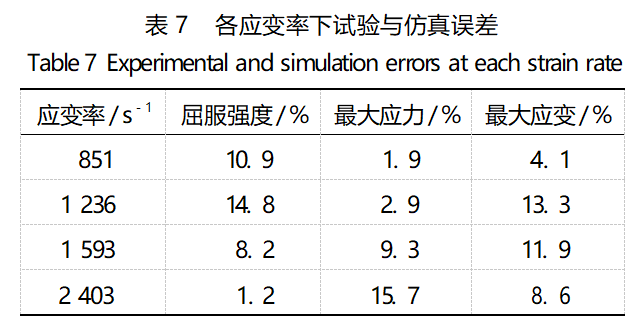
4 EFP成型仿真试验
4．1 EFP仿真模型
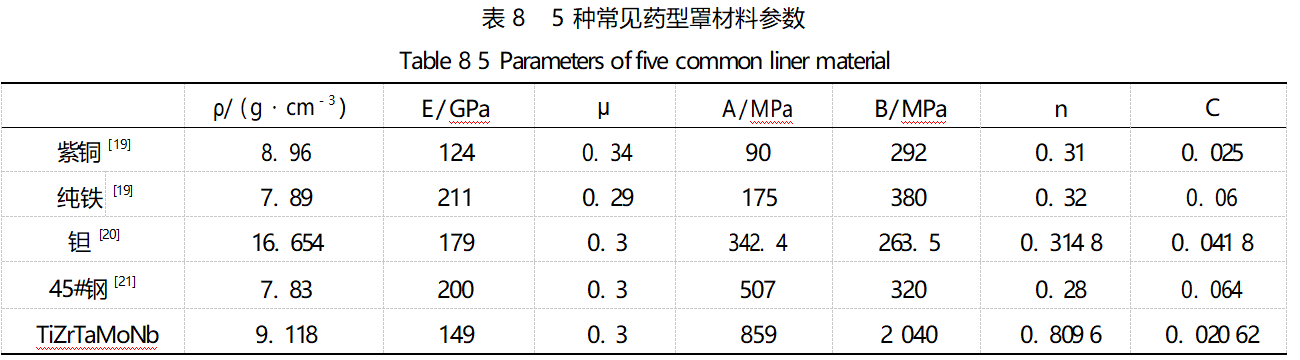
研究人员一直致力于寻找兼具高延展性和高强度的材料，以求同时满足聚能装药成型和侵彻效果两方面的要求。高熵合金因其多主元成分和简单固溶体结构，具有高硬度、高强度、以及良好的热稳定性等优良性能，具有作为弹药战斗部材料的可能性。为了研究TiZrTaMoNb高熵合金应用于EFP的可行性，建立EFP有限元模型，并选取几种常见药型罩材料(表8)，将TiZrTaMoNb高熵合金和常见材料的成型效果进行对照。

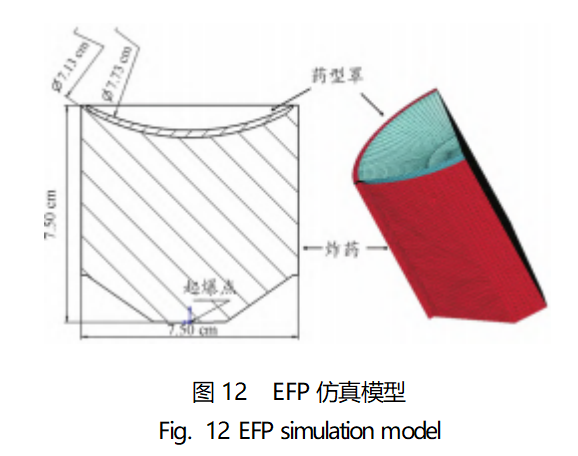
计算使用药型罩为变壁厚球缺型罩，罩顶壁厚δ=0．25
cm，内外曲率半径分别为7．73、7．13cm。采用圆柱形装药，端部为船尾形，装药直径D=7．5cm，装药长径比L/D=1;使用JH-2炸药(8701)，装药密度1．71g/cm3［18］;建立1/4对称模型如图12所示。

为了对以上5种材料的EFP成型效果进行对照比较，引入“长径比”和“密实度”的概念［22－23］。典型EFP如图13所示:EFP弹丸可以分为前端密实的头部和后端中空的尾翼2部分;D指头部最大直径，L为弹体全长，H是密实头部长度;L/D用以表征EFP的长径比，H/L用以表征EFP的密实度。

4．2 仿真结果分析
5种材料的EFP成型过程如图14所示。成型过程中，在25μs时炸药已经完成爆轰，此后炸药对药型罩变形影响很小，EFP的成型主要依靠药型罩的自锻行为，因此可利用重启动分析删除炸药部分，避免因为炸药网格畸变导致计算中断;在25～100μs内，药型罩继续发生变形，形成最终形状的EFP弹丸。较为明显的变化是:在爆轰波作用下，周围微元向罩顶汇聚，并在速度差的作用下逐渐拉伸变长，最终形成致密的头部，边缘部分逐渐向轴线收拢形成尾翼。
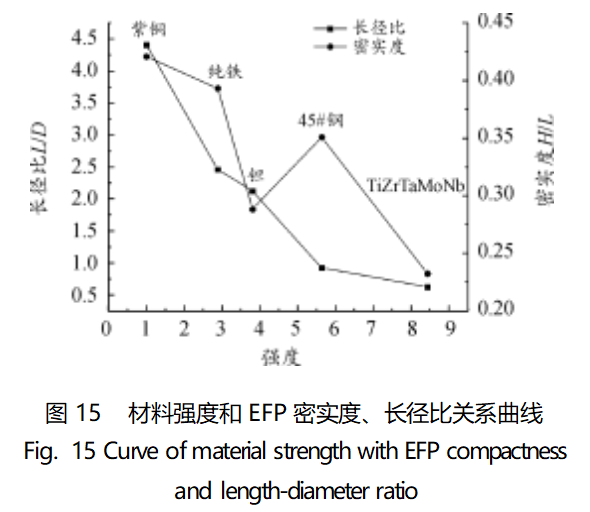
以各材料和紫铜屈服强度的比值代表材料的强度，将材料强度和长径比、密实度的关系曲线绘制如图15所示。
结合图14、图15可以看出，其他条件都相同的情况下，强度较低的紫铜、纯铁和钽形成的EFP弹丸的长径比和密实度相对45#钢和TiZrTaMoNb都要较高，形成头部密实度较高的细长弹丸。对于强度较高的45#钢和TiZrTaMoNb合金，长径比和密实度都相对较低，更倾向形成密实度较低的半球形弹丸。由此可见，随着材料强度的升高，成型效果越来越差;长径比、密实度与材料强度之间成负相关。

本文所研究的TiZrTaMoNb高熵合金在目前药型罩形状下成型效果较差，长径比和密实度较低，其成型模式为向前翻转型。主要原因在于:材料强度较高，球缺罩罩顶高度较小，在爆轰波加载下以材料强度为主，应变率效应较低;成型过程中各微元径向压缩速度衰减较快，周围质量不能在径向速度作用下向罩顶汇聚;并且轴向速度梯度较小，内外壁速度差不明显，罩顶部不能在轴向速度差的作用下拉伸成为细长且致密的头部。由此，可以通过改变药型罩罩顶高度，提高各微元径向压缩速度和轴向速度梯度，使微元向罩顶汇聚并拉伸形成长径比和密实度较高的EFP弹丸。
4．3 药型罩结构优化
影响变壁厚球缺罩成型效果的因素主要有:罩顶壁厚、罩顶高度、罩壁厚梯度、以及装药长径比。在装药条件不变的情况下，EFP弹丸成型效果主要受药型罩的形状参数影响，而球缺罩罩顶高度和罩壁厚梯度均由内外曲率半径决定。因此，可以通过调整球缺罩内外曲率半径来实现EFP弹丸成型效果的优化。EFP弹丸长径比和密实度与药型罩内外曲率半径存在以下关系:EFP弹丸密实度与药型罩内曲率半径呈正相关，与药型罩外曲率半径呈负相关;EFP弹丸长径比与药型罩内外曲率半径均呈负相关［30］。
由图14可以看出，对于强度较高的TiZrTaMoNb高熵合金，EFP成型方式为变形程度相对较小的向前翻转式，药型罩单元未发生极端变形。对于此类成型方式的EFP，失效参数对其成型过程的影响相对较小，通常不使用材料的失效模型［24］;并且有较多学者在研究聚能装药结构参数对EFP成型的影响过程中使用未加失效的本构模型，取得了较为可信的结果［25－29］。为了保证后续优化过程中各工况的可信度，需要对EFP仿真模型添加失效模型。由于缺少TiZrTaMoNb高熵合金失效参数的相关实验，无法给出准确的失效参数。因此结合式(11)和图14仿真结果所得应变率粗略估计最大失效应力;图14中TiZrTaMoNb高熵合金在EFP成型过程中应变率约为20562s－1，根据计算最大失效应力约为3525．57MPa。在仿真模型中使用MAT_ADD_EROSION关键字控制材料失效，以此作为TiZrTaMoNb高熵合金失效的判断依据。
固定装药条件和药型罩顶部壁厚不变，根据以上关系对内外曲率半径进行调整，优化后成型效果如图16所示，密实度、长径比如图17所示。

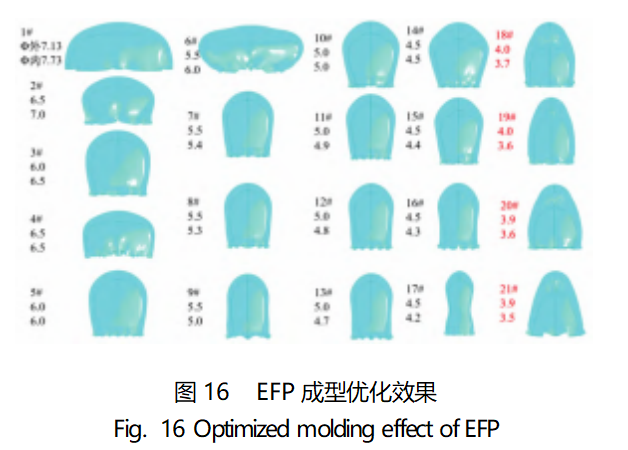
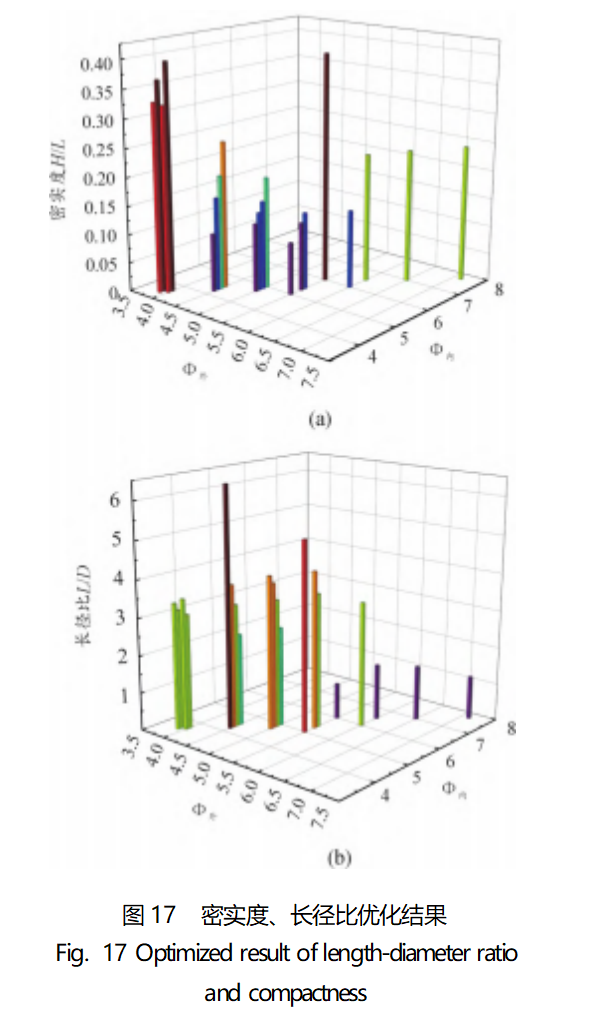
由图16可以看出，通过调整药型罩内外曲率半径可以对EFP外形产生较大改变，当药型罩内外曲率半径由工况1#改变到工况21#时，EFP弹丸的密实度和长径比都得到较大改善。在图17(a)中，对(Φ外6．0cm、Φ外5．5cm、Φ外5．0cm、Φ外4．5cm、Φ外4．0cm、Φ外3．9cm)六组工况组间进行比较，可以发现密实度随着外曲率半径减小而升高;在六组工况组内进行比较，可以发现EFP密实度随内曲率半径减小而降低。在图17(b)中，可以发现成型后的EFP弹丸长径比与内外曲率均呈负相关。以上变化关系与文献［30］所总结规律一致。
由以上优化过程可以证明，通过调整药型罩内外曲率半径，可以使EFP弹丸长径比和头部密实度得到提高。并且材料在EFP成型过程中也并未发生断裂，表现出较好的延展性。在21个工况中，工况18#、19#、20#、21#成型的EFP弹丸效果较优，其中工况18#(密实度为0．4，长径比为3．06)与图15中紫铜(密实度0．42，长径比4．40)较为接近，验证了TiZrTaMoNb高熵合金用作EFP的可行性。
5 结论
使用万能试验机和分离式霍普金森压杆对TiZrTaMoNb高熵合金进行了静、动态压缩试验。根据试验数据拟合得到Johnson-Cook模型参数，使用LS-DYNA数值模拟软件验证了拟合参数的有效性。基于所拟合参数，选取装药直径为7．5cm的EFP模型验证TiZrTaMoNb高熵合金用于EFP药型罩的可行性。得到以下结论:
1)通过静态压缩试验，得到了TiZrTaMoNb高熵合金在常温下的屈服强度、弹性模量及应力－应变关系。该材料在静态条件下具有较高强度，屈服强度约为859MPa;动态压缩试验表明，该材料存在应变率强化效应，屈服强度随着应变率升高而升高。
2)选用Johnson-Cook本构模型，使用试验数据拟合得到部分参数。基于SHPB试验，建立1/4对称模型对所拟合参数进行验证。仿真结果表明:所拟合的参数可以反映材料在应变率851～2403s－1范围内的应力应变关系。
3)选取装药直径为7．5cm的EFP仿真模型，通过调整药型罩内外曲率半径，可以得到长径比和头部密实度较好的EFP弹丸，验证了TiZrTaMoNb高熵合金用作EFP战斗部的可行性。
参考文献：刘建青，等:TiZrTaMoNb高熵合金动态特性与应用研究
星尘科技采用射频等离子体球化技术制备的TiZrTaMoNb高熵合金粉具有高球形度、低氧含量、粒度分布均匀等特点，流动性优异（霍尔流速≤标准值），适用于3D打印（如SLM/EBM）、热等静压等工艺。该粉末在高温下表现出高强度、抗蠕变和耐腐蚀性，主要应用于航空航天（涡轮叶片、燃烧室）、医疗器械（骨科植入物）及核工业等领域。相比传统方法，其无电极污染、批次稳定性好，成本降低30%-40%，可替代进口高端粉体。