孔隙缺陷对3D打印点阵结构压缩行为影响研究

发布时间:

2025-08-12

0 引言
水面舰船易遭受爆炸冲击波载荷毁伤[1-3]，随着工业技术的不断发展，船舶防护结构对轻量化的需求日益迫切。实现结构轻量化通常采用两种方法：一种是通过材料减重，采用轻金属材料、复合材料等轻质材料来改善整体结构质量[4]；另外一种是通过结构减重，如蜂窝夹层结构[5-8]、泡沫结构、折纸结构等来实现结构的轻量化[9-10]，这些新型防护结构有些因其独特的形状，很难使用传统加工方式制备。3D打印技术由于其独特的加工方式，成为目前复杂防护结构加工的优选方法。
选择性激光融化（selectivelasermelting，SLM）是一种比较成熟的3D打印技术[11]。然而，在模型加工过程中通常会产生温度梯度，导致加工成型的模型产生残余应力[12]，并可能出现孔隙、气孔和融化不完全等缺陷[13-14]。这些缺陷会降低制备构件的密度，产生应力集中，从而影响其性能[15]。为了减少金属增材制造中产生的缺陷，通常可以通过选择适当的工艺参数来限制缺陷的形成[16-17]。
例如，付立定等[18]通过SLM工艺参数的正交实验优化了加工参数，提高了316L钢材料试件的密度。Li等[19]研究了扫描速度对316L钢材料成型质量的影响，发现扫描速度越小，孔隙数量越少，尺寸也越小。Cherry等[20]研究了激光功率对316L钢材料成型质量的影响，结果表明，随着激光能量密度的增加，孔隙率逐渐降低。这些研究表明，SLM成形质量与制备工艺参数密切相关，通过改良工艺参数可以提高加工件的质量。
在研究材料内部孔隙率对力学响应的影响方面，一些学者[21-22]将延性损伤模型与有限元模拟相结合，考虑了初始孔隙率对损伤演变的影响，并发现有限元仿真结果与试验结果具有良好的一致性。微观损伤力学认为，韧性金属材料在成型和加工过程中的损伤可以通过内部微观孔隙的成核、生长和聚结过程来描述[23-24]。Gurson[25]提出了一种包括孔隙体积分数（VVF）的延展性金属塑性屈服函数，Tvergaard和Needleman对其进行修改和完善，形成Gurson−Tvergaard−Needleman（GTN）微观损伤模型[26-27]。该模型将材料的宏观力学行为与孔隙率的体积分数联系起来，从而能够将微观结构变化与宏观力学性能变化联系起来。许多研究证明，GTN模型为金属的延性损伤行为研究提供了重要参考[28-29]。然而，由于损伤参数受到结构内部缺陷的影响，内部的VVF难以准确测量，因此同一材料的损伤模型无法适用于所有3D打印模型。
本文将采用SLM制造方法制备316L钢材料拉伸件和点阵结构，并分别开展其拉伸试验和压缩试验。通过中央复合设计（CCD）–响应面法（RSM）设计试验，对GTN损伤参数进行标定，并优化得出适用于316L钢材料模型的损伤参数。最后，基于标定后的损伤参数，开展点阵结构的数值仿真计算，并结合试验分析孔隙缺陷对点阵结构压缩性能和力学的性能影响。
1 模型设计及加工
1.1 结构设计
本文设计的点阵结构由单胞模型以4×4×1的排列组成。单胞由以下部分构成：上层金字塔形结构、上层外框及内部十字交叉基座、下层金字塔形结构以及下层外框和十字交叉基座。该模型主要由5参数定义，分别是：外框高度、中心杆宽度、金字塔斜杆厚度、金字塔高度以及斜杆倾斜角度。此外，还有胞元长度这一参数。模型的具体尺寸如图1所示。图中数值单位为mm。

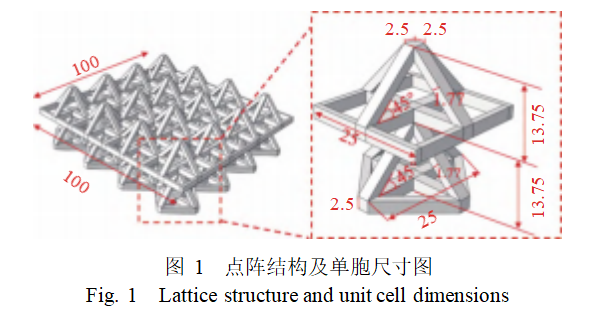
1.2 结构加工
试验模型以316L不锈钢粉末为原材料，采用SLM工艺制备。316L粉末的化学成分见表1。SLM的主要加工工艺参数包括激光功率、扫描速度、扫描间距和铺粉厚度。具体参数设置如下：激光功率260W、扫描速度1200mm/s、扫描间距0.1mm、铺粉厚度0.04mm。加工成型的模型如图2所示。
表1

2 模型试验
2.1 材料单轴拉伸试验
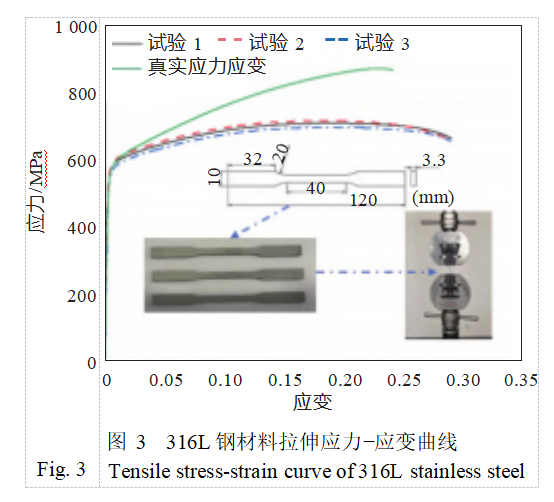
为准确测定基体材料的拉伸力学性能，采用相同3D打印工艺制备3个拉伸件。在武汉理工大学船海与能源动力学院的力学实验室，使用WDW-100型微机控制电子式万能试验机，在室温条件下对拉伸件力学性能进行试验。试验时加载速度设定为2mm/min。图3所示为测得的应力−应变曲线。由此，可确定316L钢材料的杨氏模量和屈服强度分别为203.85GPa和582.46MPa。

2.2 点阵结构压缩试验
使用WDW-300微机控制电子式万能试验机对点阵结构受压力学性能进行了研究，结果如图4所示。为了研究点阵结构受压过程中的变形和力学性能，对316L不锈钢试件进行了恒定加载速度为2mm/min的压缩试验，并记录了压缩位移、反作用力以及变形行为进行了记录。通过压缩试验得到的应力−应变曲线如图5所示。可见，整个压缩过程可以分为Ⅰ~Ⅳ这4个阶段。

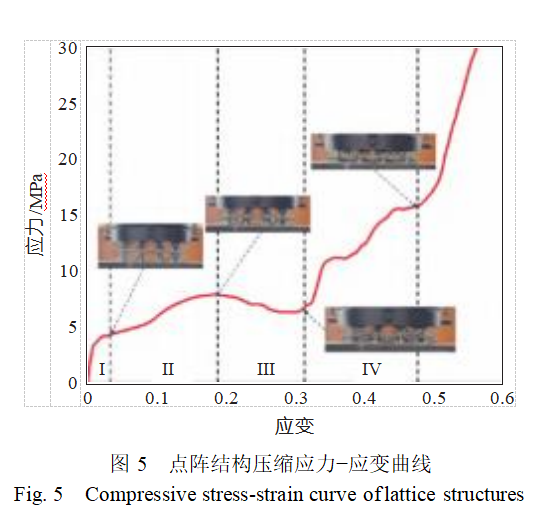
1）初始弹性阶段Ⅰ：应变范围为0～0.025。在此阶段，应力－应变曲线呈近似线性关系，应力不断上升。上面板接触结构最高点，整个结构受到压缩载荷，但整体结构未发生大变形，上层胞元开始发生变形。
2）塑性变形阶段Ⅱ：随着面板持续下降，点阵结构开始发生塑性变形和失效。当应变达到0.173时，出现第1个峰值，峰值应力为7.8MPa。此时，上层胞元十字支撑结构发生弯曲变形，直至应变值达到0.192，上层斜杆开始弯曲变形。
3）屈服变形阶段Ⅲ：应变范围为0.192～0.32。在此阶段，应力呈下降趋势。上层胞元中的斜杆已发生塑性屈服，并持续发生塑性变形。上层胞元顶端压缩到与下层胞元顶端接触，但尚未完全与底部接触，因此整体结构在高度方向上仍被压缩，直至下层胞元斜杆开始发生变形。此外，左右两边的上层胞元弯曲变形程度更大，并且与底部相接触。
4）致密化阶段Ⅳ：应变范围为0.32～0.48。在此阶段，应力逐渐上升。上层胞元底端与模型底端相接触，下层胞元斜杆完全变形。当应力达到15.62MPa时，应力急剧增加，试件进入致密区，整体模型被压扁。
3 316L钢材料模型GTN损伤参数求解
3.1 GTN损伤模型
本文采用GTN模型作为损伤模型。该模型考虑了结构制造过程中产生的内部缺陷，并在连续弹塑性模型的基础上描述了金属材料的韧性损伤和断裂过程。GTN损伤模型通过考虑孔洞的成核、生长和聚结机制，量化了孔洞对试件破坏的贡献[30]。损伤模型的方程表示为

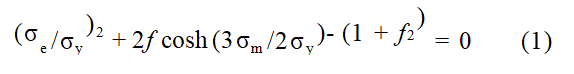
式中：σe为宏观等效应力（vonMises应力）；σy为基体材料的屈服应力（无孔洞时的屈服强度）；σm为宏观静水应力；f为当前孔洞体积分数。
Tvergaard和Needleman在Gurson模型的基础上进行补充了和完善。他们发现原有的Gurson模型无法很好的描述金属材料变形后期承载力快速下降的过程。因此，他们引入了3个修正系数q1，q2和q3，以及等效孔洞体积分数的概念。适用于各向同性强化材料的GTN屈服函数具有以下形式：

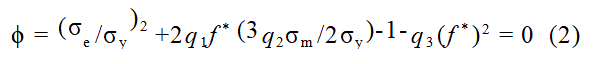
式中：f*为一个分段连续函数，用于描述材料颈缩过程中微孔洞的贯通聚合。当材料内部的孔洞体积分数f达到贯通准则所确定的临界值时贯通发生，在损伤模型中f将由f*所替代：

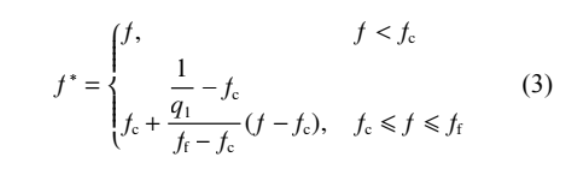
式中：fc为孔洞开始变形时的临界孔洞体积分数；ff为材料断裂时的孔洞体积分数。
损伤变量用一个标量即孔洞体积分数来表示，孔洞体积分数的增长来源于2个部分:

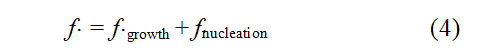
式中：fgrowth表示孔洞增长引起的孔洞体积分数比的变化率；fnucleation表示孔洞形核引起的孔洞体积分数比的变化率。根据质量平衡原理，假设基体是不可压缩的，孔洞的增长依赖宏观塑性变形，fgrowth与塑性应变的静水分量有关，可以表示为

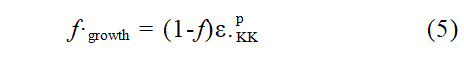
式中：ε.表示塑性体应变率，其中，上标p代表塑性相关的物理量属性，下标KK一般是指标记张量相关的约定，在连续介质力学张量运算中，常通过这种重复指标表示对张量分量的求和。
新孔洞成核的主要依靠第二相粒子或夹杂物在界面处发生断裂或脱位，由应变主导的孔洞形核准则为

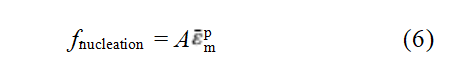
式中：A为孔洞形核系数，是基体等效塑性应变的函数，服从正态分布：

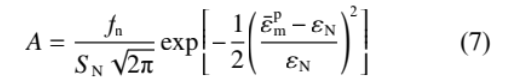
式中：fn为孔洞形核体积分数；εN是孔洞形核时的平均等效塑性应变；SN是该正态分布的标准差；
3.2 响应面模型建立
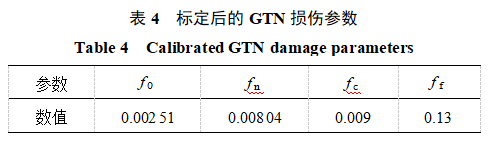
本节采用响应面法，基于中心复合设计，给出各因素与响应变量之间关系的多项式模型，并以试验结果为目标计算最优参数。GTN损伤模型中有9个参数待确定，分别是：f0，fn，fc，ff，q1，q2，q3，SN和εN。其中，q1，q2，q3是与材料性能相关的修正系数，可以通过经验确定。根据参考文献[31]，取q1=1.5，q2=1.0，q3=2.25，SN=0.1。后续主要通过响应面法确定剩余4个损伤参数：初始孔隙率f0、孔洞形核体积分数fn、临界孔洞体积分数fc和断裂孔洞体积分数ff。根据参考文献[30]选定参数范围如表2所示。

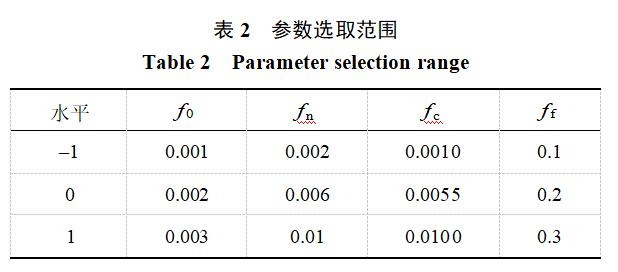
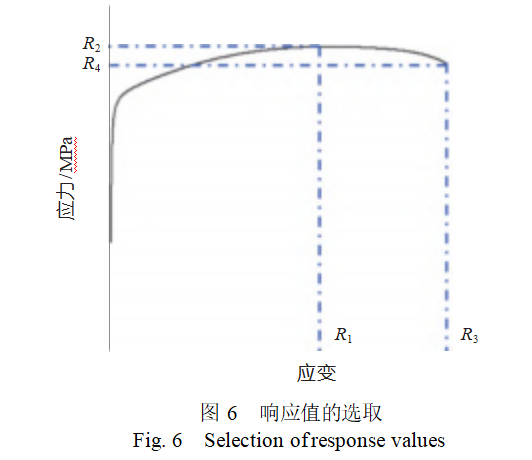
将拉伸应力−应变曲线的应力最大点和断裂点这两个点视为应力−应变曲线的特征点。应力−应变曲线中特征点的4个关键值：最高点应变R1、最高点应力R2、断裂点应变R3、断裂点应力R4作为响应值，如图6所示。4个影响因素为f0，fn，fc和ff。在Design-Expert软件中，采用四因素三水平的中心复合设计方法，设计了28组单向拉伸的仿真工况。

通过Abaqus/Explicit对单轴拉伸试验进行了有限元仿真。试件的几何尺寸与实际试验尺寸保持一致，有限元模型如图7所示。在仿真中，选用了C3D8R八节点线性六面体单元。为了提高仿真的精度，对中间拉伸区间段内的网格进行了加密，网格尺寸为0.5mm。试件左右固定面的网格尺寸为1mm。在两种不同尺寸的网格之间，设置了过渡网格以确保网格的平滑过渡。整个模型的网格总数为6400个。为了施加载荷和边界条件，在试件两端设置了参考点，并将这些参考点与试件的两端表面进行了耦合。试件的左端参考点被设置为完全固支边界条件，而右端参考点（RP-1）则施加了位移载荷。

3.3 RSM模型参数校准
在28组试验工况中，提取每组应力−应变曲线上相对应的变量，统计结果如表3所示。采用二次和三次多项式回归模型分析响应变量最高点应变R1、最高点应力R2、断裂点应变R3、断裂点应力R4。
响应面模型结果分析表明，模型显著性水平<0.001，这表明模型具有统计学意义。多元相关系数R2>0.95，说明模型数据拟合效果良好。在评估模型中各因素的显著性后，剔除了回归模型中对响应变量不显著的项。所得编码回归方程如下所示：

通过比较编码方程每个因素的系数，可以评估它们的相对影响。其中。高水平为正值，低水平为负值。通过分析可知，在4个影响因子中，fc和ff对拉伸应力−应变曲线影响大，f0和fn对拉伸应力−应变曲线影响小。
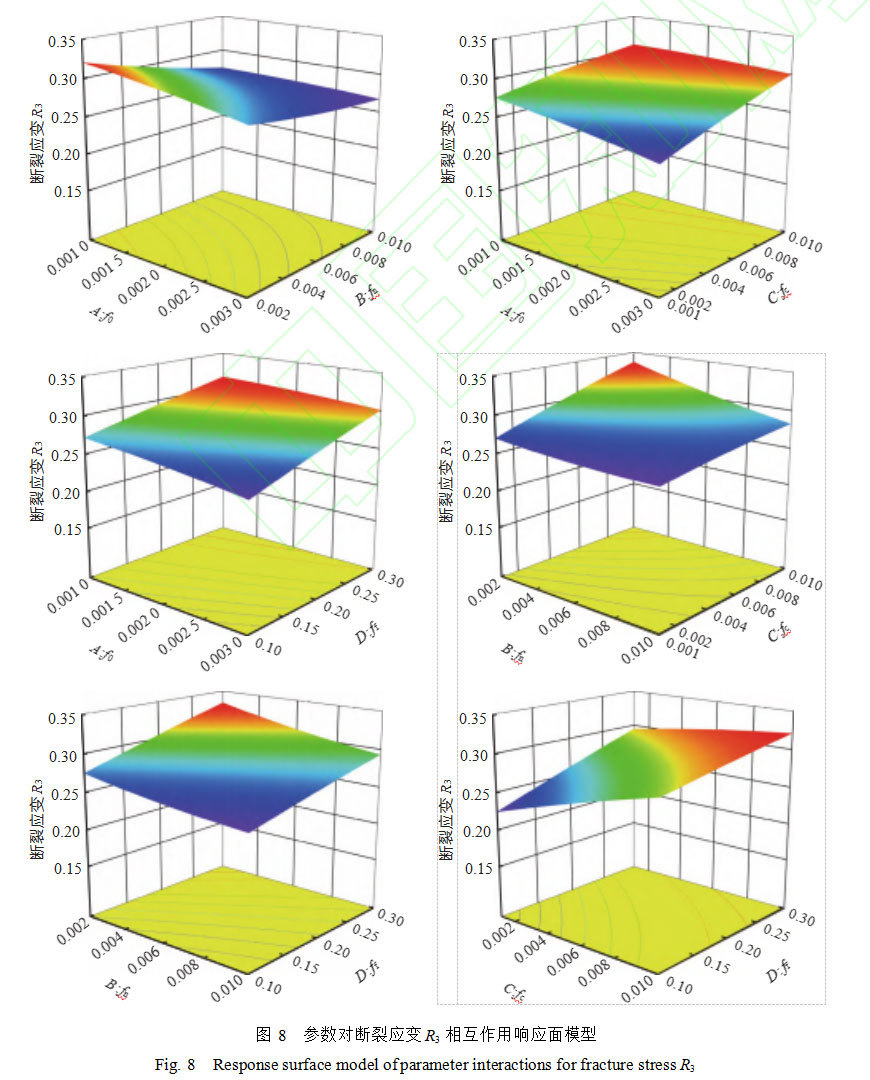
图8展示了出拉伸断裂点应变（R3）与各个参数之间的联系。从响应面曲线可以直观地显示变量与每个参数之间的关系。此外，通过观察响应面曲线可以发现，参数对拉伸断裂点应变（R3）影响趋势具有如下特点：随着fc的增大，材料断裂时的应变增大。究其原因在于，fc决定了材料内部孔隙凝聚的体积分数。在孔隙凝聚发生时，孔隙VVF会增加至ff的值。同时，随着fn的增加，断裂发生在较小应变下。这表明材料的孔隙成核体积分数的增加导致了VVF快速增长。
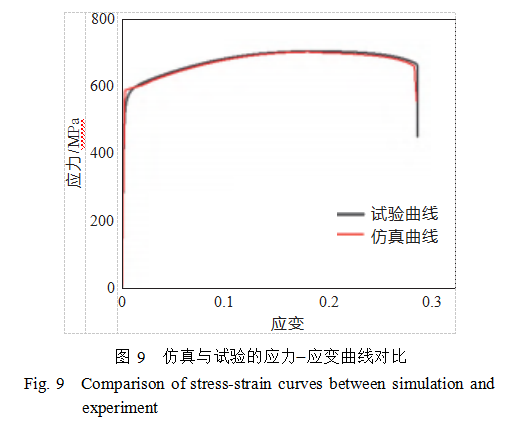
以拉伸试验应力−应变曲线中的特征点（最高点应变R1、最高点应力R2）和断裂点（断裂点应变R3、断裂点应力R4）作为优化目标。通过软件优化计算，得到了适用于316L钢材料的GTN损伤参数。具体参数见表4。利用标定后的损伤参数，对316L钢材料进行拉伸数值仿真，并将数值仿真结果与试验得到的力−位移曲线进行对比，如图9所示。从图中可以看出，仿真结果与试验结果具有良好的一致性，表明标定后的GTN损伤模型能够有效预测SLM增材制造的316L钢材料。

4 孔隙缺陷对结构力学性能影响
4.1 拉伸件CT扫描图
SLM制备加工成型的模型大多存在孔隙等内部缺陷。为了更直观的观察孔隙分布，采用CT扫描技术对拉伸件进行了检测。通过累积断层扫描图像捕捉试件的空腔，如图10所示。从CT扫描结果可以看出，整个模型存在孔隙缺陷，且孔隙分布比较均匀。
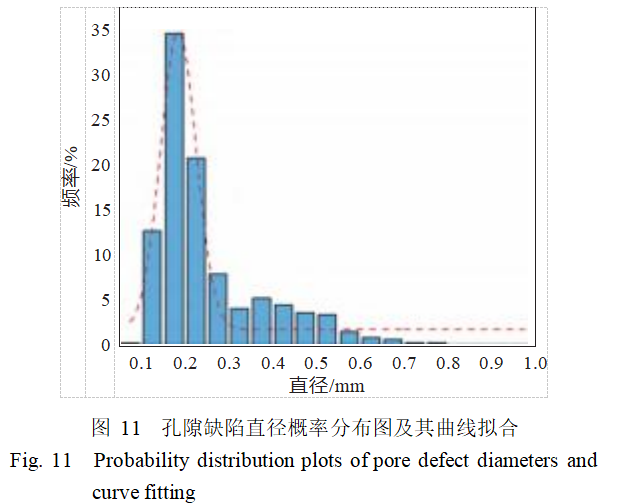
在SLM工艺中，金属材料的熔化和凝固速度极快，导致熔池内的气体没有足够时间逸出表面，从而在熔池中形成气孔。通过分析试件的内部缺陷，可以提取包括缺陷尺寸、分布和形态在内的统计数据。结合CT重建和空腔统计发现，虽然空腔的形状各不相同，但球形度主要集中在0.5～0.65之间，孔隙直径基本小于1mm，其中0.15～0.2mm的孔隙直径数量最多，直径区间占比达到34.63%，如图11所示。
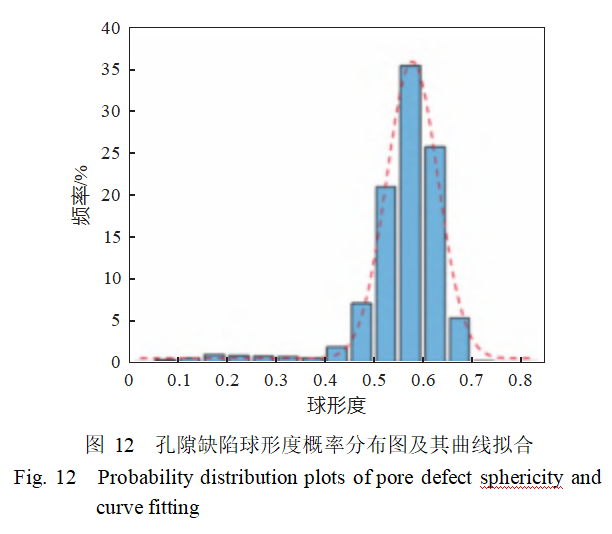
此外，球形度在0.5～0.7之间的孔隙缺陷约占87.141%，其中球形度在0.55～0.6之间的孔隙数量最多，直径区间占比为35.375%，如图12所示。
图13展示了拉伸件断裂面的扫描电子显微镜（SEM）图像。通过这些图像可以观察到结构内部存在的孔隙缺陷，这些内在缺陷会对材料的力学性能产生不利影响。此外，断裂面上还存在韧窝分布，这表明试件发生了韧性断裂。在孔洞周围还存在更小的孔洞，称为二次孔洞。二次孔洞在初始孔洞周围的剪切带上形成，通常位于小粒子附近。它们加速了孔洞之间的聚合和贯通，最终导致试件完全断裂分离。

4.2 孔隙缺陷对失效行为影响
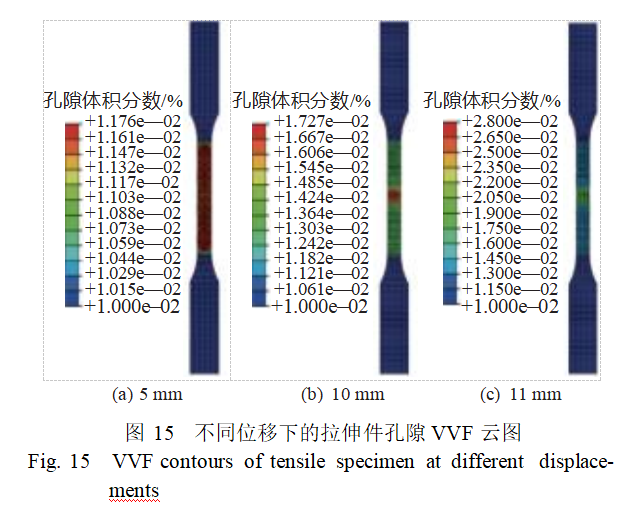
基于标定后的GTN模型参数开展拉伸件仿真计算，图14对比了拉伸试验与仿真结果，拉伸断裂位置比较吻合，说明GTN损伤模型能有效预测结构断裂损伤，损伤参数适用于SLM加工的316L拉伸件。图15显示了单轴拉伸件在紧缩断裂过程的VVF分布演变。根据试件孔隙体积分数云图，当拉伸位移为5mm时,试件孔隙体积分数为0.0117，孔洞体积分数较小。试件处于均匀变形阶段，试件孔隙体积分数在拉伸区间分布均匀，损伤积累较小。当试件拉伸位移为10mm时,试件内部孔隙体积分数扩大为0.0172，试件内部孔洞开始形核并快速增长，试件孔隙体积分数增加，这是因为孔洞聚集使得试件的变形逐渐集中。当试件拉伸位移为12.6mm时，试件内部孔隙体积分数扩大为0.028，试件内部孔隙开始形核并快速聚合长大，试件孔洞体积分数迅速增加，孔洞聚集使得试件的变形逐渐集中。图16显示了拉伸件紧缩处孔隙VVF云图，孔隙首先集中在缩颈区域，而且在横截面的中心区域尤为明显。

为了提升计算效率，减少计算时间，同时保障计算精度，对点阵压缩有限元模型进行了网格敏感性分析。分别使用网格尺寸为2.0，1.5，1.25，1.0，0.75和0.5mm的有限元模型进行了数值仿真计算，计算结果如图17所示。从图中可以看出，当网格尺寸小于2mm时，仿真结果较为接近。综合考虑计算时间和精度，最终选择1.0mm作为有限元模型的网格尺寸。

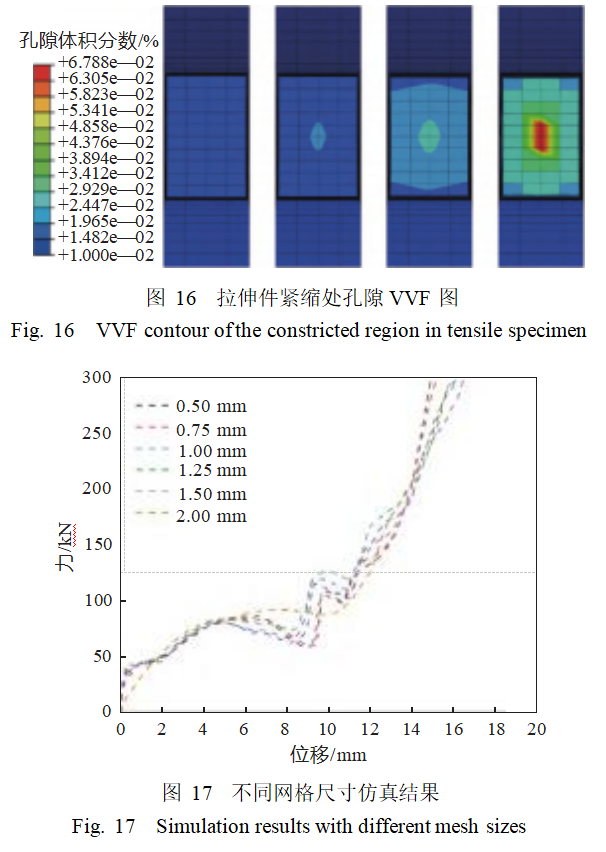
图18对比了点阵结构压缩试验和采用含孔隙模型、无孔隙模型数值仿真的力−位移曲线结果。从图中可以看出，两种仿真计算曲线都呈现出力先增加后下降，随后又增加的趋势，这与试验结果较为吻合。与无孔隙模型相比，含孔隙模型的仿真结果更接近试验曲线。在压缩位移达到0.075mm之前，有无孔隙的结果差别较小。随着载荷的持续施加，含孔隙模型的力逐渐小于无孔隙模型，且差距逐渐增大。根据GTN理论，产生此现象的原因是，随着变形的增加，局部应力变大，孔隙VVF也随之增加。当孔隙达到临界空洞体积分数时，孔隙开始聚结成大空腔，从而对结构的力学性能产生更大的影响。在初始弹性阶段，孔隙率越小，内部孔隙对材料各向同性的影响越小。图19显示了vonMises等效应力和孔隙体积分数分布云图。由图可知，在压缩变形过程中，应力集中出现在上半部分胞元十字交叉基座的中心处，同时孔隙成核也在相同区域，这导致结构更容易发生失效损伤。

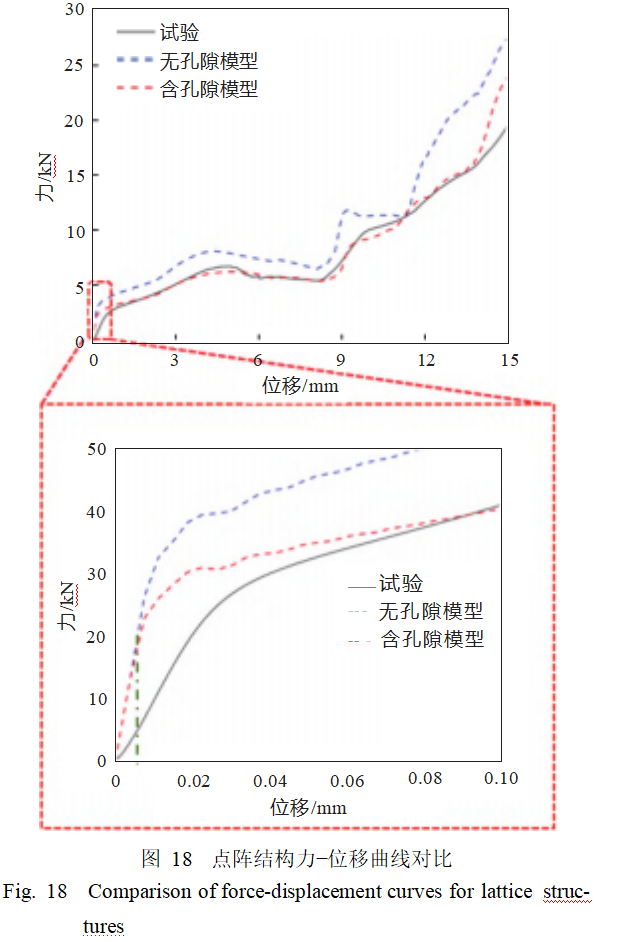
图20对比了仿真和试验结果中点阵结构在不同压缩应变下的变形模式。当应变达到0.05时，上层胞元的十字交叉基座开始变形。当应变增加到0.15时，上层胞元的十字交叉基座发生弯曲变形。当应变进一步增加到0.3时，左右两边的胞元基座与下层胞元接触，上层胞元顶端与下层胞元相接触。当应变达到0.5时，结构达到密实区，整体模型被压瘪。在相同应变下，试验结果与仿真计算结果相吻合。在压缩过程中，结构的压缩变形主要发生在胞元斜杆和十字交叉基座，整体变形呈现对称规律。中间两组胞元的变形过程较为相似，左右两组胞元的变形过程也较为相似。从图21中标红的部分可以看出，点阵结构的上下两个胞元都发生了较大的弯曲变形，上层胞元与下层胞元压缩至贴合，上层胞元的基座和斜杆都发生了大幅度的塑性变形。

4.3 孔隙缺陷对点阵结构吸能影响
对于点阵结构，能量吸收（EA）是评估其性能的主要指标，它取决于相对密度、结构几何形状和材料特性。能量吸收性能可以通过压缩变形结果获得的应力−应变曲线下的面积积分来推导。比能量吸收（SEA）表示每单位质量吸收的能量，能够更直观地反映点阵结构的吸能效率。
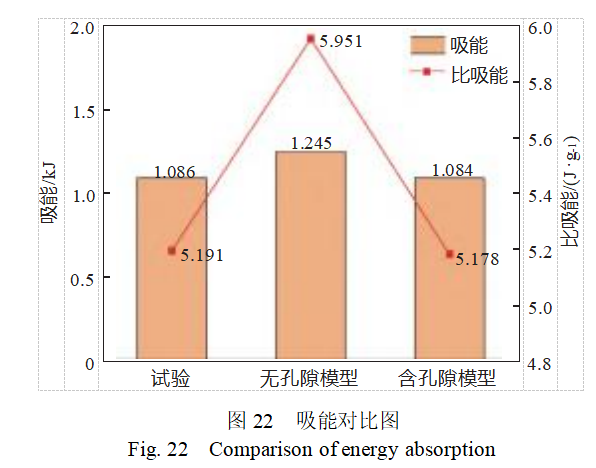
为了探究含孔隙缺陷模型对试验模型能量吸收的预测能力，图22展示了试验、无孔隙模型和含孔隙缺陷模型的能量吸收对比柱状图。实际吸能与理论值的差异主要源于加工工艺引入的内部孔隙缺陷。无孔隙模型由于未考虑内部孔隙缺陷，其能量吸收和比吸能均为最高；而含孔隙缺陷模型的能量吸收结果与试验值更为接近。三组工况对比显示，试验、无孔隙模型和含孔隙模型的能量吸收分别为1.086，1.245和1.084kJ，比吸能分别为5.191，5.951和5.178J/g。含孔隙模型与试验值的能量吸收误差仅为0.25%，而无孔隙模型与试验值的误差则高达14.6%。这一结果表明，含孔隙缺陷模型能够有效预测含缺陷点阵结构的能量吸收能力。

4.4 孔隙率对点阵结构吸能影响
针对不同孔隙率，开展了准静态压缩仿真数值计算，分别计算孔隙率为0.01%，0.1%，0.25%，0.5%，0.75%和1%的6种不同孔隙率的点阵结构。计算结果如图23所示。在应变范围0～0.1内，各曲线较为接近，应力随应变缓慢上升，表明在低应变阶段，不同孔隙率的材料响应差异不大，材料整体处于弹性变形阶段，应力与应变近似成线性关系。在应变范围0.1～0.4内，曲线出现一定程度的分离，应力−应变变化趋势出现差异。随着应变增加，应力上升趋势并非持续稳定，存在波动起伏。随着孔隙率增大，曲线出现第一处峰值应力逐渐降低。无孔隙模型的初始峰值应力为8.12MPa，而孔隙率为1%的模型初始峰值应力为5.92MPa，下降了27%。当孔隙率为0.01%时，准静态压曲线与无孔隙模型基本一致，此时孔隙对结构力学性能影响较小。

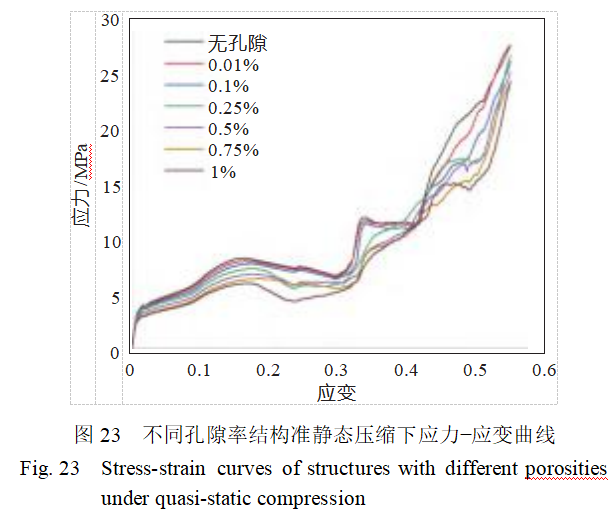
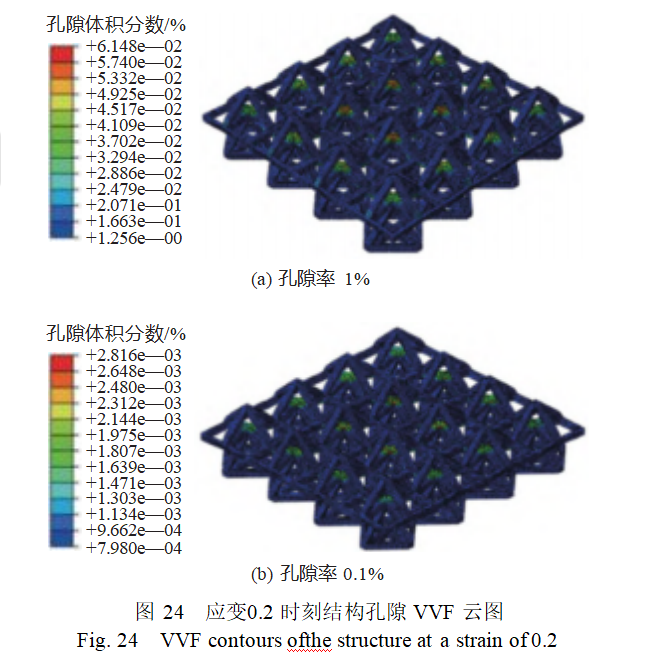
图24展示了孔隙率为0.1%和1%时，结构在应变0.2时刻孔隙VVF云图。通过对比分析可知，当孔隙率为1%时，结构内部的孔隙体积分数要大于孔隙率低的情况，这会导致结构压缩过程中应力下降，结构压缩性能降低。

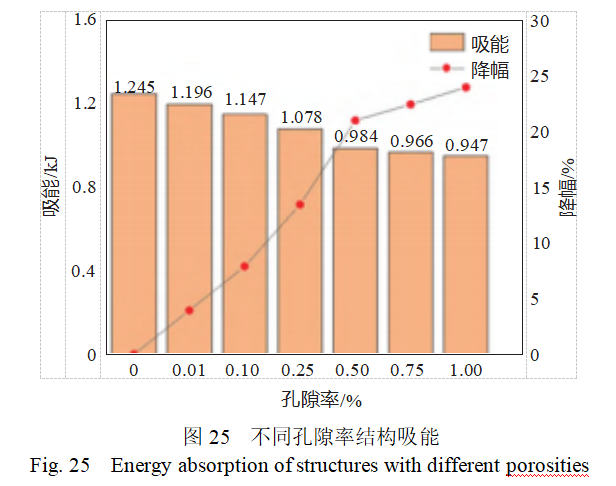
从结构吸能对比图可知，随着孔隙率的增大，结构能量吸收分别为1.245，1.196，1.147，1.078，0.984，0.966和0.947kJ，分别计算结构吸能的降幅分别为3.93%，7.87%，13.41%，20.98%，22.41%和23.94%，如图25所示。从图中可以看出，随着孔隙率增加，结构吸能降低。当孔隙率为1%时，最大降幅达到了23.94%，这一结果进一步证实了孔隙率对结构压缩性能的显著影响。

对于防护结构来说，结构吸能降低超过20%可视为结构存在较大问题。当孔隙率超过0.5%时，结构吸能降幅均大于20%。因此，为保证防护点阵结构的力学性能，最好将加工的内部孔隙率控制在0.5%以内。为了降低孔隙率对点阵结构压缩性能的影响，在结构设计之初，可以避免锐角、窄槽等易产生阴影效应的位置，必要时可以通过增加工艺圆角来减少加工过程中孔隙的产生，从而提高模型的压缩性能。
5 结论
本文采用SLM增材制造方法制备了316L钢材料拉伸件及点阵结构，开展材料力学拉伸试验和点阵准静态压缩试验。通过响应面法校准材料损伤参数，开展准静态压缩下点阵结构变形模式与能量吸收特性研究。得到的主要结论如下：
1）通过响应面模型对316L钢材GTN损伤参数进行标定，以试验应力−应变曲线最大应力点和断裂应变点为目标，校准出最合适的损伤参数，校准后模型能准确预测含孔隙缺陷试件断裂损伤和损伤演化。
2）增材制造过程中产生的内部孔隙缺陷会影响结构的力学性能。含孔隙缺陷点阵结构压缩过程中，在应力集中区域，孔隙最先开始聚结成大空腔，从而降低点阵结构强度、承载能力和能量吸收能力降低。
3）含孔隙缺陷模型能很好地描述点阵结构压缩失效过程并预测点阵结构能量吸收。因考虑了点阵结构中内部孔隙的影响，含孔隙模型和试验模型的能量吸收分别为1.084和1.086kJ，吸能相差为0.25%。
4）随着孔隙率增加，结构压缩过程应力降低，能量吸收减少，压缩性能变弱。当孔隙率加到1%时，结构吸能为947J，相比无孔隙模型吸能减少了23%，结构压缩性能受到显著影响。
参考文献：《中国舰船研究》网络首发论文孔隙缺陷对3D打印点阵结构压缩行为影响研究
星尘科技专注于稀有难熔金属球形粉末的研发与生产，产品具有高纯度、低氧含量和优异球形度等特点，同时提供粒度、成分等参数定制服务。公司依托先进的粉末制备技术，为客户提供增材制造（3D打印）全流程解决方案，涵盖材料开发、工艺优化到成品加工等环节。我们坚持技术创新与质量控制，致力于为航空航天、医疗器械、精密模具等领域客户提供专业可靠的粉末材料及增材制造服务。欢迎咨询郑经理13318326187.