TiZrNbHf难熔高熵合金的层裂行为

发布时间:

2025-09-30

引言
随着科技的发展，传统的合金在高温、高压、辐照、高应变率等极端情况下的力学性能指标已经不能满足现代社会发展需要。为此，高熵合金作为一种新兴的多组元合金开始逐渐引起关注，成为了前沿热门的研究领域。其概念最初分别由Yeh1和Cantor2提出，通常指代由4种或4种以上的等摩尔比或者近似摩尔比的元素组成的一类合金[2-4]。由于HEAs的自由成分以及由此产生多样的显微结构，因而其通常表现出不同于传统合金的力学性能。事实上绝大多数HEAs的力学性能都要优于传统金属，尤其是在极端的动态条件下，包括高速冲击和动态剪切[5,6]。例如典型的Cantor合金，即FeCoNi-CrMn HEA在应变率为2.3×10³s⁻¹的拉伸测试中极限抗拉强度为734MPa,延伸率约为63%[7],在应变率10³s-¹下，最大屈服强度也能达到700MPa8,TiZrNbV⁹]、TiZrHfNbTa10,11]、TiZrHfNbTaW12]、Al-Mo.5NbTao.5TiZr1³3]等难熔高熵合金(Refractory high-entropy alloys, RHEAs)在应变率10³s⁻¹以上时的最大屈服强度也都在1000MPa以上。含能材料是一类在高温或者在高压下能够发生化学反应并释放出大量能量的材料[14-16]。含Ti、Zr等易氧化金属的难熔高熵合金作为含能结构材料有着巨大的潜力，例如TiZrNbVRHEA⁹]在高速冲击时发生剧烈燃烧，发生氧化反应释放出大量的热量，有着良好的冲击释能特性。
在材料内相向运动的两个稀疏波交汇瞬间所叠加的拉伸应力超过材料的抗拉极限时便会在内部产生裂纹的现象称为层裂现象。平板撞击实验是研究材料层裂现象的重要手段。研究材料在极端加载下的力学行为，是其在未来工程应用中的重要基础。材料的动态机械性能取决于材料的加载应变率以及微观结构，例如化学有序以及晶格畸变等。通过对Fe₅₀Mn₃₀Co₁₀Cr₁0高熵合金的动态层裂损伤进行研究，王海民等[17]发现孔洞成核点集中在基体部分，且裂纹会避开高阻抗的马氏体区域。Hawkins等[18]对不同Al含量的FeCrMnNi高熵合金的静动态拉伸响应进行了研究，发现静态下由于AI、Ni金属间化合簇的出现，导致材料从塑性逐渐向脆性转变，其相同加载条件下的动态拉伸强度与材料内部在奥氏体附近的铁素体项有关，较高的铁素体项占比会导致基体内部的孔洞成核点更多，在成核过程中能更好地消耗掉内部的能量，导致材料内部小孔洞占比增加，但是总孔洞占比降低，最终提高材料的动态拉伸强度。Zhang等[19通过平板撞击实验研究了FCC相Alo.1CoCrFeNiHEA的冲击压缩和层裂行为，发现层裂强度与其加载应变率之间存在幂律关系，位错滑移和层错堆垛是其变形的重要机制，并且在高速冲击下观察到了纳米孪晶。其发现该HEA的损伤是延性损伤，孔洞优先在晶粒内部成核并且晶内空隙表现出对晶界取向差和峰值应力的强烈依赖性。Cheng等[20]对CoCrFeNiHEA研究发现其损伤为延性损伤，冲击引起的位错滑移和变形孪晶主导塑性变形。随着冲击速度的增加，位错密度显著增加，开始出现孪晶束。对于层裂早期，孔洞优先在晶界处成核，特别是在晶界的三重接点处。Ren等[21]对TiZrNbVRHEA研究之后发现其动态变形受到位错滑移、位错扩散、变形带交叉和晶粒细化的控制，沿晶、穿晶和混合型裂纹是其层裂破坏的主导形式，动态霍尔-佩奇效应和晶格畸变引起的钉扎效应导致了高动态屈服强度。其研究发现，声子拖曳效应的临界应变率与金属的相对原子质量和局部应变场正相关。在实验载荷范围内，RHEA表现出良好的结构稳定性，同时基于冷能混合物的状态方程理论计算方法可以准确预测其冲击响应行为。价电子浓度(VEC)对HEA的冲击压缩性能有直接影响，VEC越高意味着压缩HEA的难度越大。
本研究中使用20mm一级轻气炮平台进行了非对称平板撞击实验，对TiZrNbHfRHEA的动态力学特性进行了探究，得到其层裂强度、Hugoniot弹性极限以及在实验冲击速度范围内的Hugoniot状态方程，并对回收试样进行了金相分析，以期为TiZrNbHfRHEA的工程应用提供参考。
1 实验
1.1 材料制备
熔炼TiZrNbHf RHEA的金属原料颗粒分别为纯度≥99.99%的Ti、Zr、Nb、Hf颗粒，其中Ti颗粒采购自湖南湘投金天钛金属股份有限公司，Zr颗粒采购自北京中金研新材料科技有限公司，Nb颗粒采购自长沙南方钽铌有限责任公司，Hf颗粒采购自北京研邦新材料科技有限公司。
在本实验中采用真空电弧熔铸的方法进行制备TiZrNbHf RHEA原始铸锭，采用的设备为沈阳科学仪器研制中心研制的DHL-1250真空电弧熔炼炉。
制备流程为：(1)将Ti、Zr、Nb、Hf金属颗粒按照等摩尔比称重并进行超声波清洗，除去表面杂质；
(2)清洗干净真空电弧熔炼炉的铜坩埚，将表面氧化物清理干净，避免杂质进入熔炼过程；(3)将清洗并干燥完毕的金属颗粒放入铜坩埚中，开始抽真空，注入保护气体氩气；(4)打开电源开始引弧熔炼；(5)首先多次翻转熔炼Ti块来吸收炉内残余氧气，避免进入熔炼过程；(6)正式熔炼TiZrNbHf RHEA,多次翻转熔炼并使用磁搅拌装置来彻底融化颗粒原料并充分混合；(7)将得到的纽扣状铸锭移动至铜模具上进行熔化吸铸成型。
将上述步骤得到的TiZrNbHf RHEA铸锭最终加工成尺寸为Φ10mm×2mm的试样。
1.2 材料结构观察
通过X射线衍射(X-ray diffraction,XRD)分析样品的相组成，X射线光源为CuKα射线管，波长λ为0.1542nm,工作电压为40kV,工作电流为40mA,扫描角度20为10°~130°,扫描速度为3°/min。扫描电子显微镜(Scanning electron microscope,SEM)用来观察合金的显微组织，通过电子背散射衍射(Elec-tron Backscatter Diffraction, EBSD)分析合金样品的晶粒分布以及尺寸分布，扫描步长为1μm,EBSD样品采用氩离子抛光。分别通过扫描电镜的背散射电子(BSE)成像和二次电子(SE)成像模式观察合金剖面形貌。
1.3 层裂试验装置
层裂试验基于20mm一级轻气炮平台进行，通过无氧铜飞片撞击TiZrNbHf难熔高熵合金靶板来完成层裂试验。平板撞击实验装置装配如图1所示。

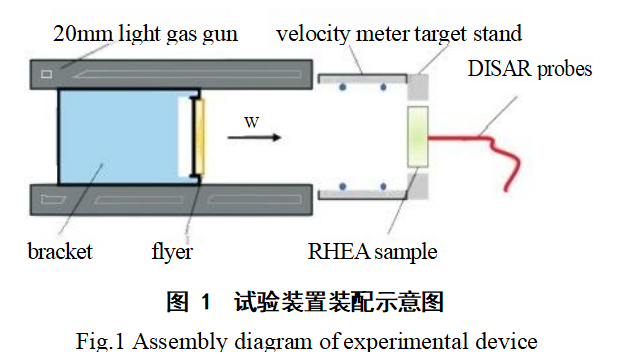
由图1可知，实验选用与TiZrNbHf RHEA阻抗相近的无氧铜作为飞片，通过聚醚醚酮弹托与飞片的配合来实现加载。通过改变一级气体炮发射仓加载气压来改变冲击速度。飞片的速度通过气体炮出口端的磁测速装置测量。无氧铜飞片的尺寸为Φ12mm×1mm,试验的速度范围为360～740m/s。TiZrNbHf RHEA靶板通过聚醚醚酮靶架固定在炮口处，在装配过程中需要保证靶板与飞片中心线位置在同一水平线上，以此保证在撞击过程为正碰。靶架背板中心位置安装光纤跳线，另一端连接全光纤激光位移干涉(Displacement Interferometer System for Any Reflector,DISAR)系统，得到试样背面(非撞击面)自由面速度变化曲线，以此来分析内部层裂行为。需要注意的是，靶板表面需要使用砂纸抛光，光纤跳线测量的一面即非撞击面需要抛光至镜面级以保证激光信号良好。
2 计算方法
2.1 材料层裂计算方法
非对称碰撞层裂试验中，在如图2(a)所示的波系图中，飞片与试样靶板高速碰撞之后分别在靶板和飞片中产生右行和左行的冲击压缩波，冲击波到达靶架自由面和飞片后界面反射产生相向运动的稀疏波，并在样品内部产生交汇区域。右行波在靶架自由面处反射，导致自由面速度从0增大至Umax,如图2(b)所示。相向而行的稀疏波在靶架内形成的交汇区域为形成的拉伸作用区。当拉伸应力超过了材料的抗拉强度时，试样内部产生裂纹，发生层裂现象，同时在试样内部产生新的自由面；与此同时已经传播过去的右行稀疏波使试样右端自由面速度降低，此后的部分拉伸波会被裂纹阻挡，再次反射的压缩波在试样端面反射导致自由面速度从up发生回跳。

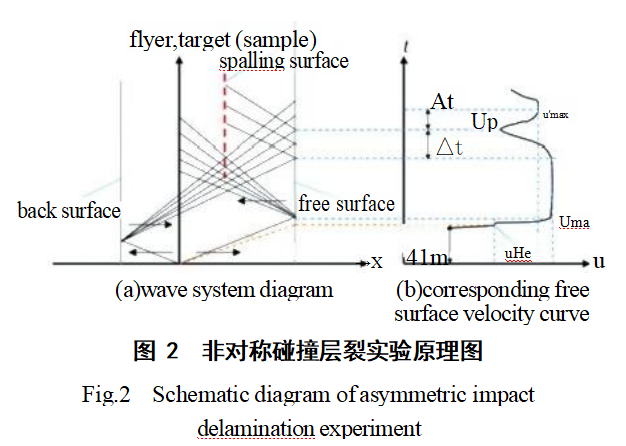
无氧铜飞片撞击TiZrNbHf RHEA靶板，在撞击过程中，试样靶板先达到Hugoniot弹性极限，Hugo-niot弹性极限定义为材料在平面冲击加载下发生弹塑性屈服时的轴向应力，记为σHL。材料的Hugoniot弹性极限可以用公式计算[22]:

式中：0H为Hugoniot弹性极限；PRE为TiZrNbHf RHEA密度；CL为常态下合金纵波声速，CL=3841m/s,在室温298K下测得；UH为弹性波粒子速度；u为自由面上先行弹性波最大速度，即自由面速度历史曲线上拐点对应的速度，UH=1/2um。
初始弹性波的应变率εH见下式：

式中：HEL点对应的应变;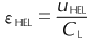△tHL为弹性压缩波经历的时间。
冲击加载的峰值压力Pmax可以通过靶板最大自由面速度umax和材料的状态方程计算得到。根据自由面速度倍增定律，右行冲击波的波后粒子速度为（式2-2），结合冲击波关系式可以得到塑性波冲击峰值压力，见下式：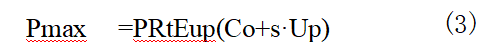

式中：Pmax为塑性波冲击峰值压力；Co和s为TiZrN-bHf RHEA状态方程参数。
根据Romanchenko等[23,24]给出的考虑层裂片厚度对层裂过程的影响，得到层裂强度计算公式，见下式：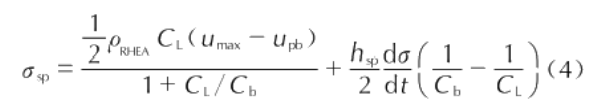

式中：hs为层裂片厚度，mm;Umx为最大自由面速度，m/s;Um为回跳速度，m/s;Cb为体积波速，m/s。
应力率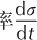以下面公式进行计算：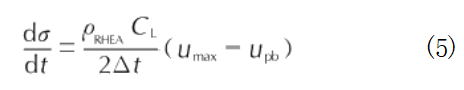

式中：△t为自由面速度从umax下降到u所经历的时间，μs。
试样在加载过程中的加载应变率见下式[25]: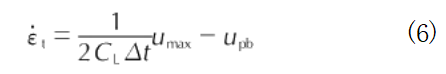

试样再加速度a,定义为试样自由面速度从回跳速度u再次增大至峰值u′mx的变化率[25,见下式：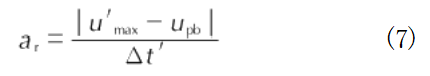

2.2 Hugoniot状态方程理论计算方法
在开始实验确定出材料力学性能之前，Hugoniot状态方程被用来预测材料性能，根据理论计算得到的数据来设计飞片和试样的具体尺寸，并选择与靶板试样阻抗相匹配的材料26]。在层裂实验中，通常使用Hugoniot数据来预估层裂强度[27-29]。本研究中使用冷能混合法来预测高熵合金状态方程。
由固态物理学可知，在中低压下，不考虑电子热运动的影响，金属晶体的总压力P+主要包括冷压Pc和热压PH,见下式：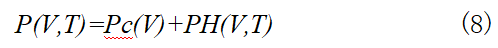

式中：比容V=1/p,p为密度；T为温度。
冷压Pc表示温度为OK时压缩金属晶格所产生的压力，取决于原子之间的相互作用，热压Pa代表原子在非0K下从平衡状态发生微小振动即原子热运动所产生的压力，该压力与材料的温度相关。以材料的冷能—冷压(Ec—Pc)曲线为参考，结合冲击波守恒关系，可以得到基于Ec—Pc曲线的冲击Hugoniot曲线[303,见下式：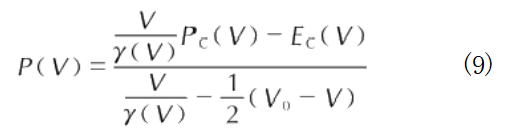

式中：Pc为冷压；Ec为冷能(即材料在温度为0K时的压力和内能);Vo=1/p。为初始比容，P。为初始密度；（式9-1）是Gruneisen系数，其为比容V的函数。
根据实验结果可以推导出的材料冲击Hugoniot曲线为直线，即材料冲击波波速D与自由面波后粒子速度up之间为线性关系[22,见下式：

式中：Co和s都为常数。
通过公式可得到基于Hugoniot状态方程的冲击Hugoniot曲线[31,见下式：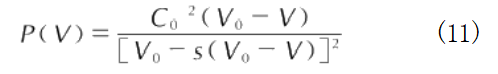

公式(9)和公式(11)给出了由冲击波守恒方程推导出的冲击Hugoniot曲线。公式(9)为冲击Hugoniot曲线的理论计算方法，公式(11)给出了基于实验结果的冲击Hugoniot曲线表达式。
Born-Meyer势可以描述金属晶体的冷压和冷能，见式(12)和式(13)32]: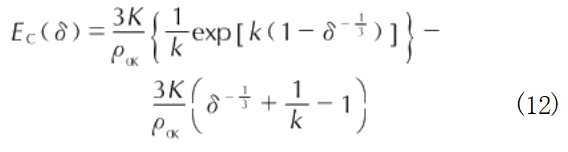

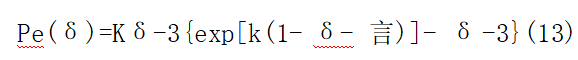
公式(9)和公式(11)给出了由冲击波守恒方程推导出的冲击Hugoniot曲线。公式(9)为冲击Hugoniot曲线的理论计算方法，公式(11)给出了基于实验结果的冲击Hugoniot曲线表达式。
Born-Meyer势可以描述金属晶体的冷压和冷能，见式(12)和式(13)32]: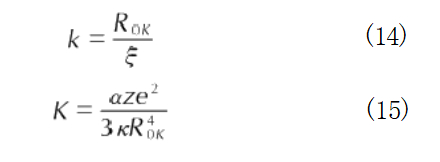

式中：R为0K时的原子平衡距离；ξ为斥力因子，取决于金属阳离子的电子结构；a为Madelung常数；e为基本电荷；z为价电子数；k为结构因子，取决于晶格结构；K和k为材料参数，综合考虑晶体的内部结构特征。
在Einstein固体模型中，固体中原子的振动可以看作是在平衡位置处微小振动的一维简谐振动。根据Dugdale-MacDonald公式34],Gruneisen系数γ(V)可以用下述公式描述：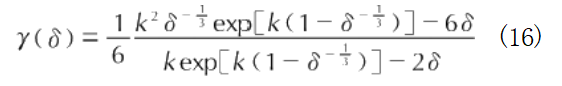

式中：K和k可以从温度为0K时的Hugoniot数据得到[35]: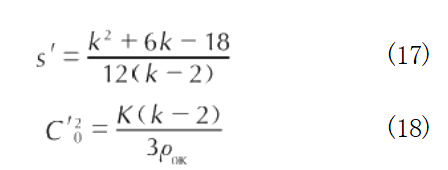

通常材料参数C。和s是在室温下进行测量，因此需要对测量得到的参数进行温度修正。材料在温度为0K时的Hugoniot参数C′。和s′可以通过下述公式进行计算[35: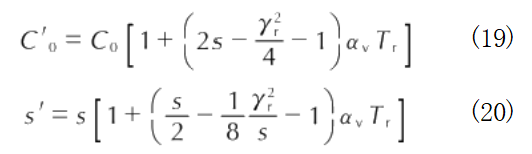

式中：α为体积膨胀系数；y.为室温下的Gruneisen系数；T,为室温。
如果冲击加载时合金中各元素的压力瞬间达到平衡状态，则可以通过质量平均特性的叠加来计算合金的冷能Ec30],见下式：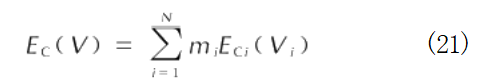

式中：m、V;、Ec;分别表示第i种元素的质量占比、比容和冷能。
在理论计算时将TiZrNbHf RHEA视为由Ti、Zr、Nb、Hf4种元素组成的均相合金，基于上述公式和假设，合金的状态方程可通过下列步骤进行计算：
(1)根据各元素的冷能—比容关系和公式，计算合金的冷能Ec;(2)根据热力学关系Pc=-dEc/dV
计算合金冷压；(3)根据上述过程计算得到的冷能—比容关系和冷压—比容关系的数据，结合公式(9)、公式(12)和公式(13),采用最小二乘法拟合出材料的参数K和k;(4)通过公式(16)计算得到Gruneisen系数γ(V);(5)最后使用公式(11)计算合金的状态方程。
3 结果与讨论
3.1 原始试样的微观结构
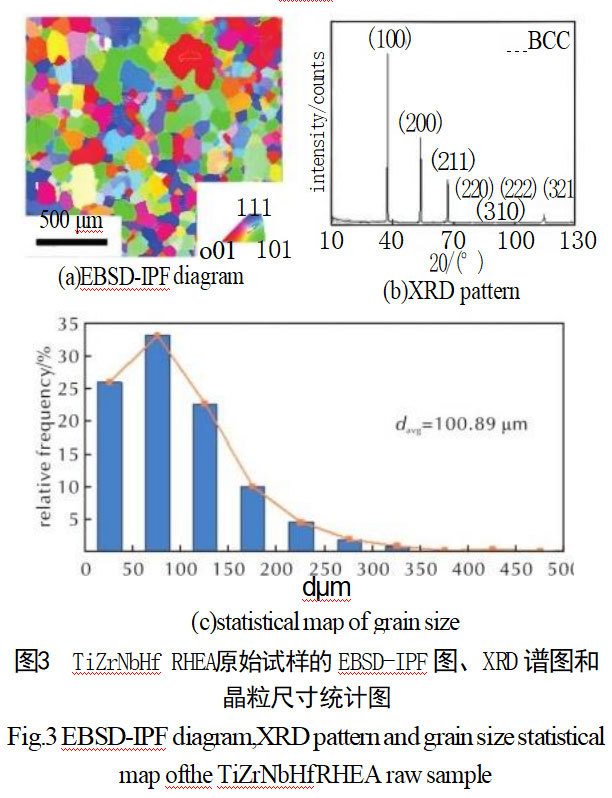
通过EBSD对原始试样进行分析，图3(a)为EBSD分析的反极图(Inverse pole figure,IPF),发现试样内部晶粒尺寸分布均匀，晶粒取向随机分布；图3(b)为XRD谱图，结果表明该合金为单相BCC结构；图3(c)为测试区域晶粒尺寸统计分布图，可以观察到晶粒尺寸主要集中在25～125μm之间，通过统计分析得到平均晶粒尺寸davg=100.89μm。

3.2 层裂行为分析
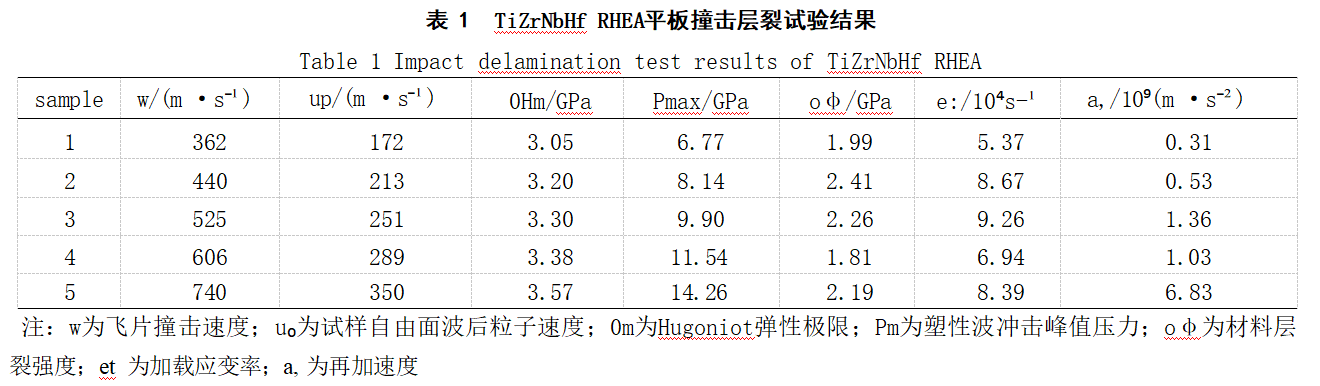
共开展5组平板撞击层裂试验，通过改变飞片撞击速度(w)来改变加载情况。up为靶板自由面波后粒子速度，根据公式(1)～公式(7)分别计算OHE、Pmax、Osp、et、a,,实验结果见表1。
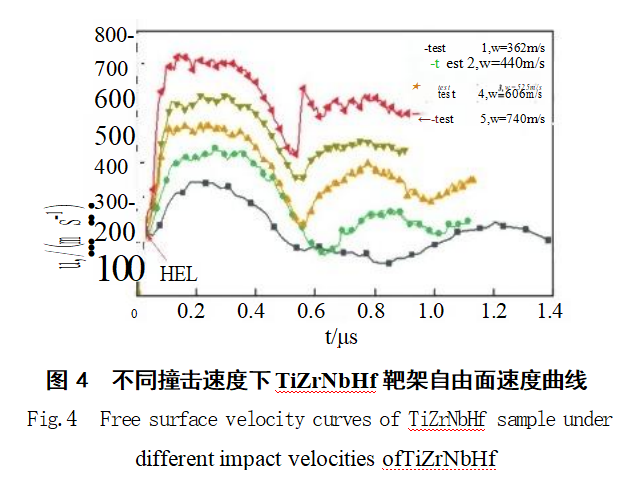
从表1中可以看出，塑性波冲击峰值压力Pmax均已经达到Hugoniot弹性极限σHL,TiZrNbHfRHEA靶板已经发生了层裂现象。不同撞击速度下TiZrN-bHf RHEA靶板自由面速度历史曲线如图4所示，曲线符合理论推导，说明试样内部出现层裂现象。飞片的撞击速度从362m/s增大至740m/s,其TiZrNbHfRHEA靶架的最大自由面速度逐渐增大至700m/s左右。试样在加载过程发生层裂，随着冲击速度的增大，靶板内部峰值冲击压力从6.77GPa逐渐增大至14.26GPa,从曲线中可以观察到不同冲击速度下加载平台宽度较为接近，约为0.20μs。计算得到TiZrNbHf RHEA的Hugoniot弹性极限oHa随着冲击速度增大而增大，从3.05GPa增大至3.57GPa。从图4中还可以观察到随着冲击速度的增大，回跳速度up出现的时间越来越早，再次回弹至最大速度u'max所经历的时间越来越短，曲线逐渐陡峭，同表1中计算的再加速度a.随冲击速度变化的趋势一致，随着冲击速度逐渐增大，a,从3.1×10⁸m/s²逐渐增大至6.83×10⁹m/s²。

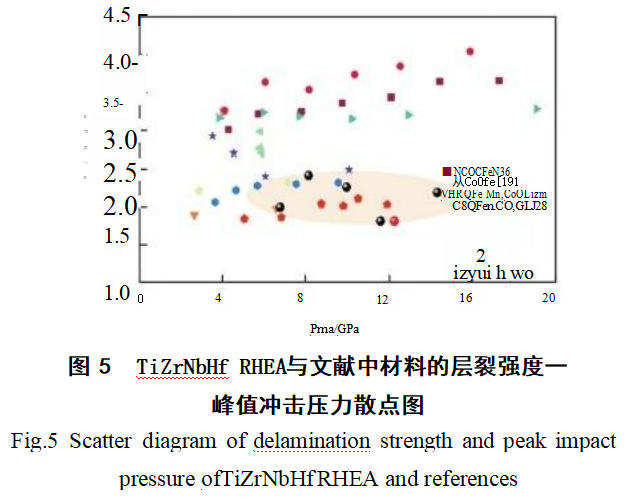
本研究的TiZrNbHf RHEA的层裂强度与Al-CoCrFeNi2.1[36、Alo.1CoCrFeNi19]、HRQFesoMn₃₀Co10Cr1[28]、CRQFe₅oMn₃oCo₁₀Cr10[28]、CrMnFeCoNi37]、CoCrFeNi[20、Fe₄oMn2₀Cr₂oNi₂。[25]、高强度钢(HSSS)[38]、TiZrNbV²¹对比如图5所示。本研究中的TiZrNbHf为单相BCC结构的难熔高熵合金，相较于3D族高熵合金，其层裂强度相对较小，层裂强度范围为1.99～2.41GPa,更容易发生层裂现象。

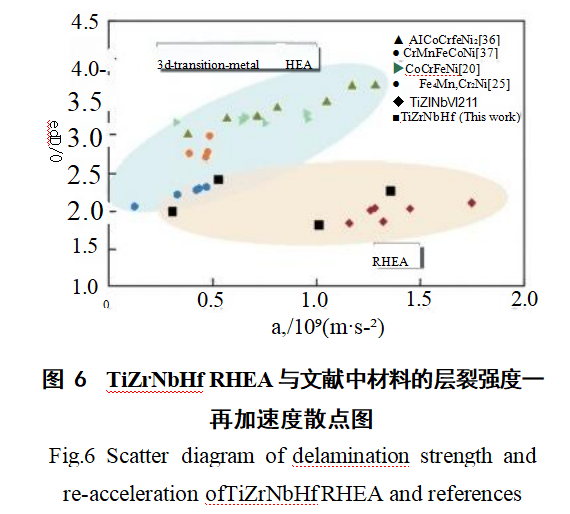
TiZrNbHf RHEA与文献[20,21,25,36,37]中材料的层裂强度—再加速度散点图如图6所示。
图6进一步说明难熔高熵合金的层裂强度普遍小于3D族高熵合金。再加速度a,反映了加载过程中的损伤率，较高的a,表明较高的空穴成核和聚结率以及较差的延展性。从图6可以观察到TiZrNbHf RHEA的层裂强度—再加速度散点较TiZrNbV21分布松散，其层裂强度稍大一些，也说明了其延展性比TiZrNbV RHEA[²¹好。

3.3 Hugoniot状态方程
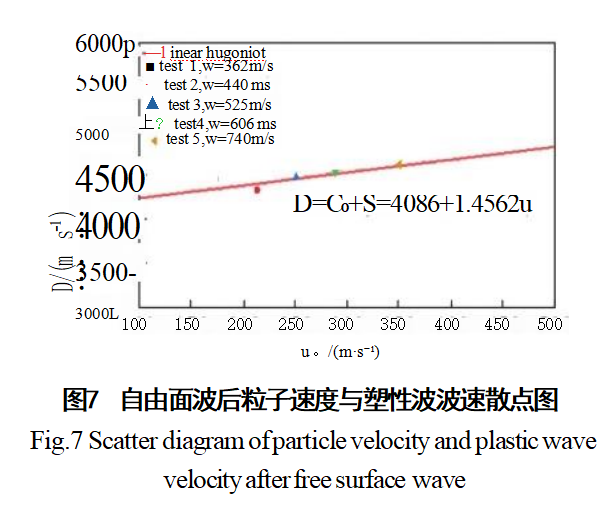
层裂试验的自由面波后粒子速度与塑性波波速散点图如图7所示，表现出线性Hugoniot关系，拟合得到冲击波波速D与自由面粒子速度up之间的关系，见下式：
D=Co+sup=4086+1.4562up(22)
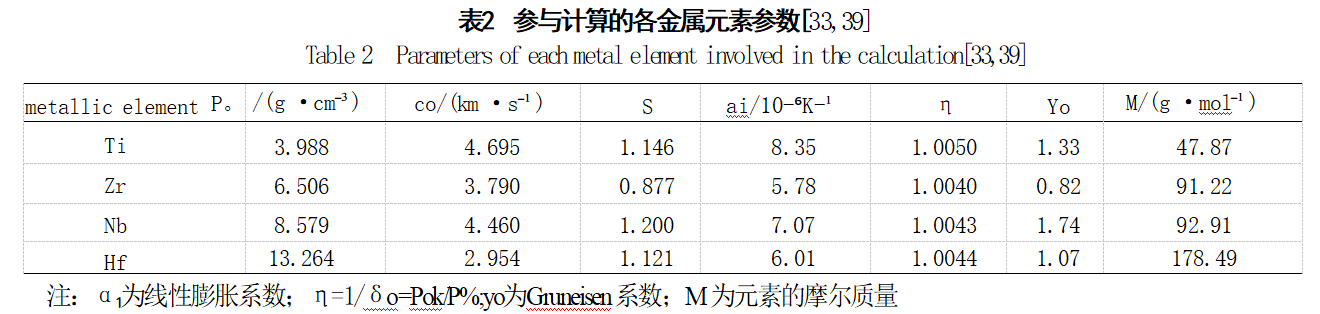
除了根据平板撞击实验得到TiZrNbHf状态方程之外，还可以利用上述2.2节中的理论方法计算其冲击压缩特性：首先根据参与计算的各金属元素参数，计算各元素的冷能—比容关系，通过公式(21)合金的冷能Ec,再根据热力学关系Pc=-dEc/dV计算合金冷压Pc,然后根据上述过程计算得到的冷能—比容关系和冷压—比容关系的数据，结合公式(9)、公式(12)和公式(13),采用最小二乘法拟合出材料的参数K和k,进而根据公式(16)计算得到Gruneisen系数γ(V),最后使用公式(11)计算合金的状态方程。关于各元素在计算时的相关参数可以参考表2[33,39]。通过上述方法可计算得到理论的K=0.7881GPa,k=6.0925,进而计算Gruneisen系数γ(V),最终得到其理论状态方程。
峰值冲击压力关于自由面粒子速度和相对比容的空间分布如图8所示，其中黑色球点为实验数据，红色曲线为基于实验数据的状态方程拟合曲线，蓝色曲线为基于冷能混合法的理论计算曲线。

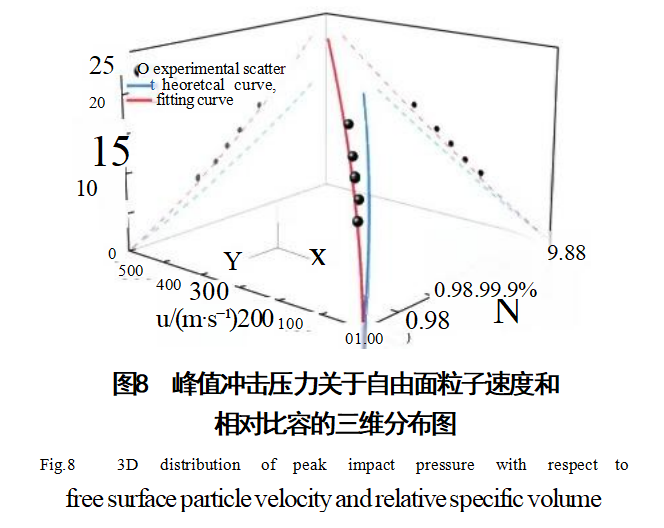
从图8可以发现，基于上述过程得到的理论状态方程与基于实验数据的状态方程存在误差，其具体表现为实验曲线在理论曲线上方，且误差随着曲线上升的趋势逐渐增大。理论方法计算得到Co,mik=3660m/s,Smx=1.1472,而实验数据得到的参数Co=4086m/s,s=1.4562,实验结果与理论计算存在偏差。理论方法在计算时的假设条件是混合时组成元素原子均匀分布，各组成元素原子的混合不会改变各原子之间的相互作用势，并且各个元素的属性被保留，然而在HEA中因为存在晶格畸变现象[4,40-44],TiZrNbHf RHEA的晶格参数发生变化，从而引起材料参数K和k发生变化，进而使得实验结果偏离理论计算[21]。理论计算结果与实验结果(拟合线)之间存在偏差，但是在自由面粒子速度小于250m/s时，峰值冲击压力关于自由面粒子速度的曲线图中理论线和拟合线之间偏差小于20%;在相对比容大于0.95时，峰值冲击压力关于相对比容的曲线图中理论线和拟合线之间偏差也小于20%,因此认为其在较低冲击速度的情况下能够起到预测材料性能的作用。
3.4 金相分析
通过对3个冲击速度440、606、740m/s的回收试样做电镜扫描分析，不同冲击速度回收试样的SE和BSE结果如图9所示。

由图9可知，440m/s的冲击速度下可以观察到试样内部孔洞相连，开始形成层裂现象，随着冲击速度增大，孔洞直径逐渐增大，在740m/s的冲击速度下，其层裂情况明显大于工况为440m/s冲击速度。
对740m/s冲击速度的回收试样做更细致的观察，结果如图10所示，可以发现孔洞相连，形成裂纹。

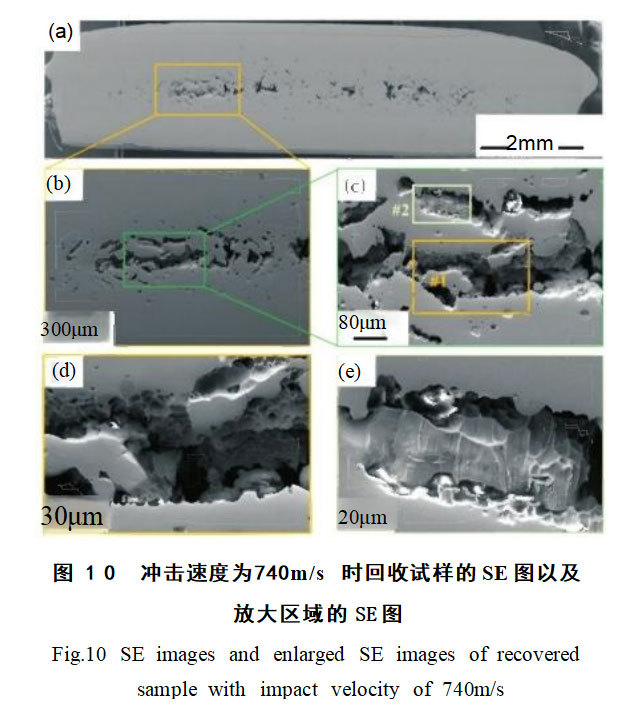
通过对该回收试样中严重损伤区域进行放大观察，如图10(b)和(c)所示；图10(d)和(e)分别为图10(c)中的区域1和区域2的放大图。从图10(c)中可以发现孔洞内存在大量的韧窝，具体如图10(d)所示，说明了其损伤模式可能是韧性断裂。在图10(c)中还发现了少部分的河流状花样，这被认为是脆性断裂的特征。综上所述，该材料的损伤模式是以韧性断裂为主的混合断裂模式。从图10(d)和(e)可知，还能在孔洞内发现因冲击压缩释放的能量而熔化的痕迹。
4 结论
(1)采用平板撞击试验研究了不同冲击速度下TiZrNbHf RHEA的动态层裂特性，在塑性波冲击峰值压力范围为0～20GPa时，TiZrNbHf RHEA的层裂强度范围为1.81～2.41GPa。
(2)TiZrNbHf RHEA的Hugoniot状态方程显示出线性关系，冲击波波速D与自由面粒子速度up之间的关系为D=Co+sup=4086+1.4562up。
(3)状态方程理论计算与实验结果由于RHEA的晶格畸变现象而存在偏差，但理论方法在实验的低速范围(自由面粒子速度低于250m/s)内仍可用来预测材料性能。
(4)回收试样微观分析表明了其损伤模式为韧性断裂为主的混合断裂模式。
参考文献：中图分类号：TJ55;O341 文献标志码：A 文章编号：1007-7812(2024)12-1104-10
TiZrNbHf难熔高熵合金的层裂行为
球形TiZrNbHf难熔高熵合金粉呈体心立方结构，具备高强度（拉伸强度超700MPa）、低弹性模量（可低至70GPa左右）及良好延展性，高温下组织性能稳定。其球形形貌赋予优良流动性与成形性，适配增材制造等工艺，且成分元素无毒或低毒，生物相容性好。相较传统合金，兼具难熔特性与综合力学性能优势。可用于生物医用植入件，也适用于航空航天等领域的高温部件制造，在3D打印、粉末冶金领域有实际应用价值。更多详情，欢迎联系我们的专业人员：郑经理13318326187.